.Problema para ajudar na escola: Traslados para um evento

✏ Link do problema para dispositivos da Apple.

Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Difícil)

Camila está organizando traslado aéreo para 1000 pessoas e 60 toneladas de bagagens, da cidade [tex]C_1[/tex] para a cidade [tex]C_2[/tex], onde ocorrerá um megaevento.
A empresa contratada para efetuar os traslados tem condições de disponibilizar doze aviões do tipo A e oito aviões do tipo B, com as seguintes características:
Aeronave A: transporta até 200 passageiros e 6 toneladas de bagagens.
Aeronave B: transporta até 100 passageiros e 15 toneladas de bagagens.
Todos os voos decolarão e pousarão, praticamente, nos mesmos horários.

(a) A princípio, considerando apenas a quantidade de aviões de cada tipo, quais as possíveis maneiras que Camila terá para organizar os traslados, independentemente de quantos e quais passageiros vão em cada avião?

(b) A locação de um avião do tipo A custa R$ 400 000,00 e a de um avião do tipo B custa R$ 100 000,00. Se Camila dispõe de R$ 2 400 000,00 para os traslados, quais são as possibilidades que ela tem? Dessas, quais as duas mais baratas? E as duas mais caras?

Observação: O problema deve ser resolvido utilizando-se um plano cartesiano [tex]xOy.[/tex]

Solução 1

(a) Sejam [tex]x[/tex] e [tex]y[/tex] as quantidades de aeronaves dos tipos A e B a serem utilizadas, respectivamente. Assim, a partir dos dados do problema, vamos estabelecer as restrições para [tex]x[/tex] e [tex]y[/tex]:

(1) Serão contratados [tex]x[/tex] do tipo A e [tex]y[/tex] do tipo B. Como cada aeronave do tipo A transporta até [tex]200[/tex] passageiros, cada aeronave do tipo B transporta até [tex]100[/tex] passageiros e [tex]1\ 000[/tex] pessoas devem ser transportadas, a capacidade de todos os aviões deve chegar, no mínimo, a essa quantidade de [tex]1\ 000[/tex] pessoas. Logo:

[tex]200x+100y \geqslant 1000.[/tex]

(2) Como cada aeronave do tipo A transporta até [tex]6[/tex] toneladas de bagagens, cada aeronave do tipo B transporta até [tex]15[/tex] toneladas de bagagens e [tex]60[/tex] toneladas devem ser transportadas, a capacidade de transporte de todos os aviões deve chegar, no mínimo, a [tex]60[/tex] toneladas. Logo:

[tex]6x+15y \geqslant 60.[/tex]

(3) Camila só dispõe de doze aeronaves do tipo A e oito do tipo B. Assim:

[tex]x \leqslant 12[/tex] e [tex]y \leqslant 8.[/tex]

(4) Por outro lado, não se pode contratar um número negativo de aeronaves. Portanto:

[tex]x \geqslant 0[/tex] e [tex]y \geqslant 0.[/tex]

Por (1), (2), (3) e (4), a solução do item (a) é dada pelos pares ordenados naturais [tex](x,y)[/tex] tais que:

[tex]\begin{cases}
x \geqslant 0 \\
y \geqslant 0\\
x \leqslant 12\\
y \leqslant 8\\
200x+100 y \geqslant 1000\\
6x+15y \geqslant 60\\
\end{cases} \, .\qquad \qquad \textcolor{#800000}{(i)}[/tex]

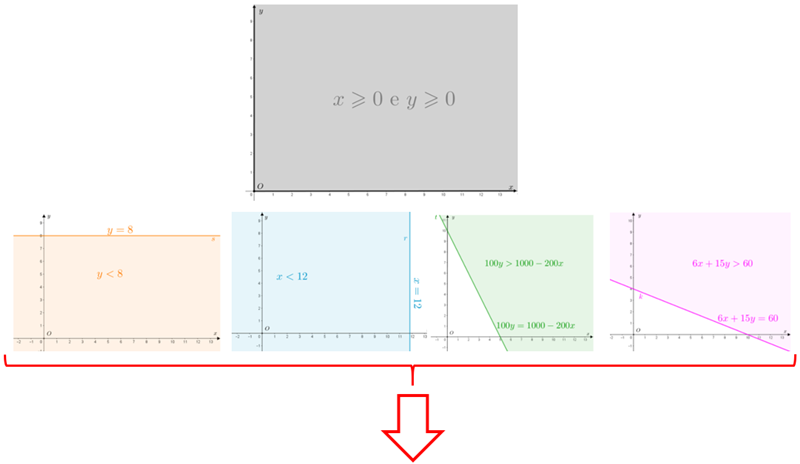
Nada impediria que construíssemos uma tabela com todos os valores naturais de [tex]x[/tex] e [tex]y[/tex] tais que [tex]x \leqslant 12[/tex] e [tex]y \leqslant 8[/tex] e avaliássemos as somas [tex]200x+100y [/tex] e [tex]6x+15y.[/tex] No entanto, seriam [tex]13 \times 9=117[/tex] situações nas quais as duas somas seriam avaliadas, ou seja, teríamos que fazer [tex]117\times 2=234[/tex] somas! Por isso é que no problema foi sugerida a utilização de um plano cartesiano [tex]xOy.[/tex] Assim, a solução do item (a) do problema são os pontos de coordenadas naturais [tex]P=(x,y)[/tex] do plano cartesiano [tex]xOy[/tex] que satisfazem simultaneamente às seguintes condições:

[tex]\boxed{x \geqslant 0 \text{ e } y \geqslant 0}\quad[/tex] ; [tex] \quad \boxed{x \leqslant 12}\quad[/tex] ; [tex]\quad \boxed{y \leqslant 8}\qquad [/tex] ; [tex]\quad \boxed{200x+100 y \geqslant 1000}\quad [/tex]; [tex]\quad \boxed{6x+15y \geqslant 60} \, [/tex].

Então, vamos estudar cada uma dessas condições isoladamente em [tex]\mathbb{R} \times \mathbb{R}[/tex], para depois analisarmos as cinco simultaneamente e obtermos as soluções cujas coordenadas são números naturais.

[tex]x\geqslant 0[/tex] e [tex]y\geqslant 0[/tex]
Os pontos [tex]P=(x,y)[/tex] que satisfazem essas duas condições são:

[tex]x \leqslant 12 \, [/tex]

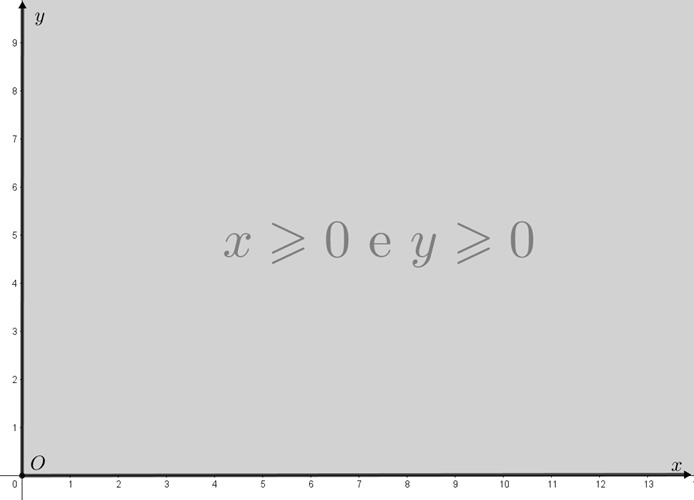
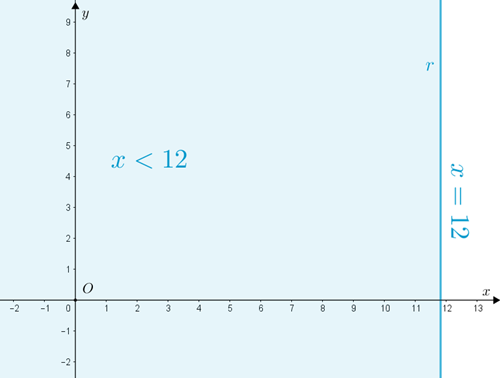
Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:

[tex]y \leqslant 8 \, [/tex]

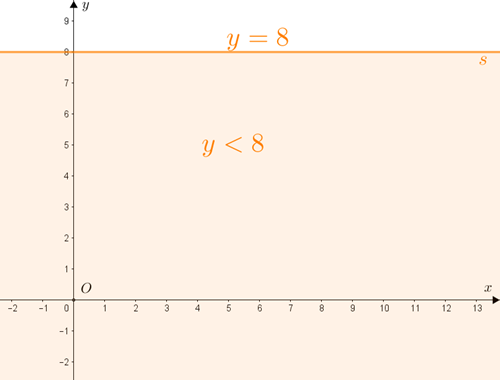
Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:

[tex]200x+100y \geqslant 1000 \, [/tex]

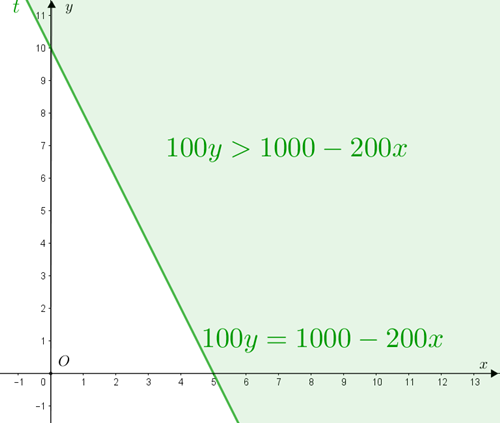
Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:

[tex]6x+15y \geqslant 60[/tex]

Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:

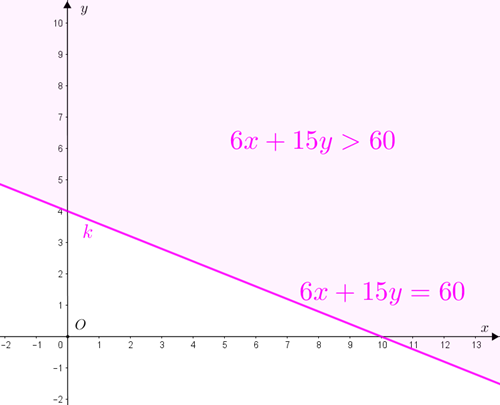
Fazendo a interseção das cinco regiões acima, e lembrando que a primeira nos obriga a trabalhar no primeiro quadrante e na parte não negativa dos dois eixos do plano cartesiano, obtemos a solução do sistema [tex]\textcolor{#800000}{(i)}[/tex] em [tex]\mathbb{R} \times \mathbb{R}.[/tex]

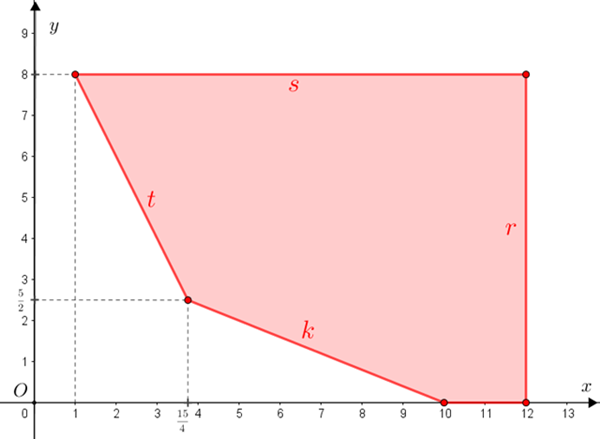
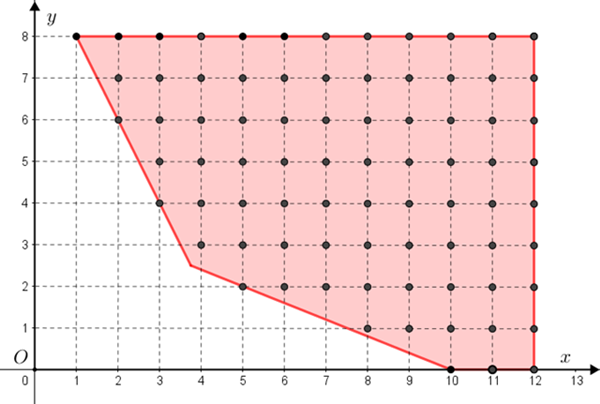
Como as opções de Camila são dadas por pares ordenados [tex](x,y)[/tex], com [tex]x[/tex] e [tex]y[/tex] números naturais, podemos contá-las na figura a seguir e concluir que ela tem [tex] \, \fcolorbox{black}{#eee0e5}{$79$} \, [/tex] maneiras para organizar os traslados, sem levar em consideração quantos e quais passageiros vão em cada avião e se a bagagem de cada passageiro vai no mesmo avião dele.

(b) A locação de um avião do tipo A custa R$ 400 000,00 e a de um avião do tipo B custa R$ 100 000,00. Assim, se [tex]x[/tex] e [tex]y[/tex] são, respectivamente, as quantidades de aeronaves dos tipos A e B a serem utilizadas nos traslados, podemos definir o custo da locação da seguinte forma:[tex]\boxed{400000x+100000y}.[/tex]
Temos, então uma função [tex]G[/tex] de duas variáveis, definida por [tex]G(x,y)=400000x+100000y[/tex], para a qual precisamos inicialmente determinar quantos dos [tex]79[/tex] pares ordenados [tex](m,n)[/tex] do item (a) são tais que [tex]G(m,n) \leqslant 2400000[/tex].
Mais uma vez, poderíamos calcular [tex]G(m,n)[/tex] para cada um dos [tex]79[/tex] pares ordenados, o que daria um pouco de trabalho. Mas note que, para cada número [tex]k[/tex], a equação [tex]400000x+100000y=k[/tex] descreve uma reta.
Assim, podemos analisar geometricamente a família de retas paralelas descritas por [tex]400000x+100000y=z[/tex], para números naturais [tex]z[/tex] variando de [tex]0[/tex] a [tex]2\ 400\ 000[/tex], no plano cartesiano no qual esteja representada a solução do item anterior.
A interseção de cada uma dessas retas com a região obtida na solução do item (a) determina os pontos que fornecem a quantidade de aeronaves dos dois tipos cujo preço de locação é o número [tex]z[/tex] que define a reta em questão.

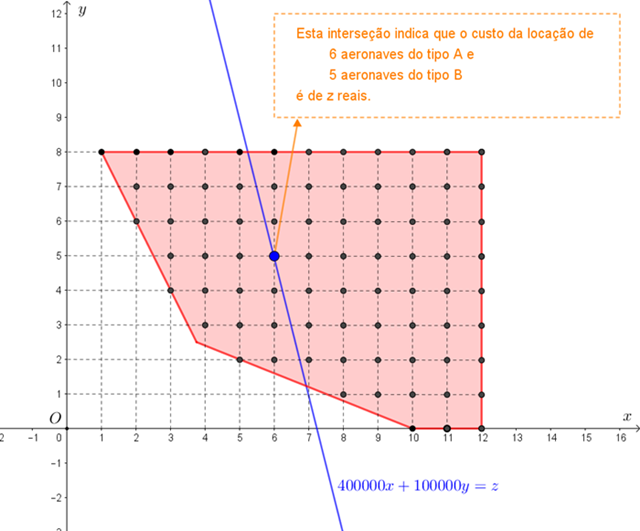
Para facilitar a análise, podemos utilizar o applet abaixo.

No aplicativo podemos visualizar um plano cartesiano [tex]xOy[/tex] e os pontos que representam as [tex]79[/tex] maneiras de se organizar os traslados segundo as condições do item (a). Vemos também a reta definida pela equação [tex]400000x+100000y=0[/tex]; esta é a primeira reta da família de retas [tex]400000x+100000y=z[/tex], na qual a variável [tex]z[/tex] representa o preço final pago pela locação de [tex]x[/tex] aeronaves do tipo A e [tex]y[/tex] do tipo B. As demais retas dessa família são obtidas movimentando-se horizontalmente o ponto que aparece na parte inferior direita do applet, sobre o segmento verde. Esse ponto indicará valores naturais de [tex]0[/tex] a [tex]2400000[/tex], valores estes que representarão preços de [tex]R\$ \, 0,00[/tex] a [tex]R\$ \, 2\ 400\ 000,00[/tex] para locação de [tex]x[/tex] aeronaves do tipo A e de [tex]y[/tex] aeronaves do tipo B.
Para cada reta obtida com a movimentação do ponto Preço, a sua equação será exibida na parte superior do applet.

Com a reta definida quando Preço[tex]=2400000[/tex] ([tex]400000x+100000y=2400000[/tex] ou simplesmente [tex]4x+y=24[/tex]), fica definida uma nova região no plano cartesiano [tex]xOy[/tex] que nos mostra quantas das [tex]79[/tex] maneiras que Camila tem para organizar os traslados custam [tex]R\$ \, 2\ 400\ 000,00[/tex] ou menos. Vejam na próxima figura.

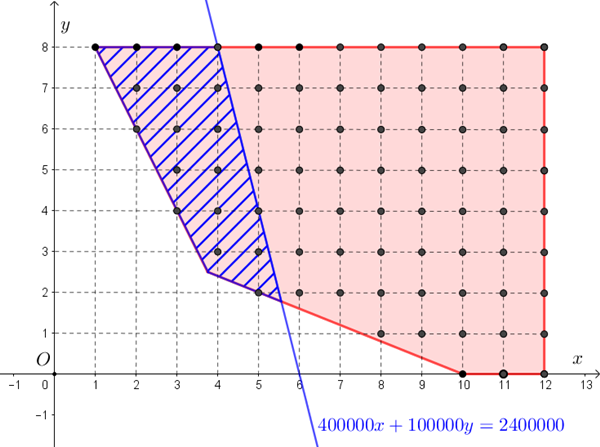
Portanto, Camila tem [tex] \, \fcolorbox{black}{#eee0e5}{$18$} \, [/tex] maneiras de organizar os traslados, respeitando o limite total de [tex]R\$ \, 2\ 400\ 000,00[/tex].
Com o auxílio do applet, podemos ver que os preços dos traslados crescem à medida que as retas [tex]r[/tex] se deslocam da esquerda para direita, assim:

as duas opções mais baratas totalizam:

[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$R\$ \, 1\ 188\ 000,00$} \, [/tex], sendo utilizadas [tex]1[/tex] aeronave do tipo A e [tex]8[/tex] do tipo B
[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$R\$ \, 1\ 400\ 000,00$} \, [/tex], sendo utilizadas [tex]2[/tex] aeronaves do tipo A e [tex]6[/tex] do tipo B;

as duas opções mais caras totalizam:

[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$R\$ \, 2\ 400\ 000,00$} \, [/tex], sendo utilizadas [tex]4[/tex] aeronaves do tipo A e [tex]8[/tex] do tipo B, ou [tex]5[/tex] aeronaves do tipo A e [tex]4[/tex] do tipo B;
[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$R\$ \, 2\ 300\ 000,00$} \, [/tex], sendo utilizadas [tex]4[/tex] aeronaves do tipo A e [tex]7[/tex] do tipo B, ou [tex]5[/tex] aeronaves do tipo A e [tex]3[/tex] do tipo B.

Solução elaborada pelos Moderadores do Blog.

Solução 2

Quem optou por fazer as contas e construir uma tabela para o item (a) e outra para o item (b) pode conferir os resultados com as tabelas que disponibilizamos a seguir.

Esta tabela foi construída para se verificar em quantas situações aeronaves do tipo A e do tipo B satisfazem as condições do item (a).

Tabela com número de passageiros e toneladas de bagagens

Esta tabela foi construída para se verificar em quantas situações aeronaves do tipo A e do tipo B satisfazem as condições do item (b).

Tabela com número de passageiros, toneladas de bagagens e preço da locação

As duas tabelas foram construídas no Excel. Disponibilizamos abaixo um arquivo contendo-as.
Abram esse arquivo e tentem entender como elas foram construídas. Observem também que é possível definirmos funções que fornecem o número de opções para cada item do problema.
O Excel é muito mais do que um editor para se formatar planilhas. Às vezes ele opera verdadeiros milagres…

Arquivo

Observação: Para abrir o arquivo, você precisa ter o Excel instalado em seu computador.

Solução elaborada pelos Moderadores do Blog.

Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo.
Você pode abrir o arquivo diretamente no seu navegador (Chrome, Edge, Firefox, Safari, entre outros), mas também pode utilizar o software gratuito Adobe Acrobat Reader.
Caso o dispositivo que você está utilizando não tenha o Acrobat Reader instalado, é só clicar AQUI para fazer o download adequado ao seu dispositivo.

Arquivo