.Problema para ajudar na escola: Uma área verde

Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)

---

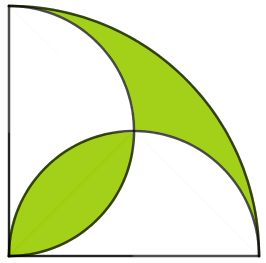
(XXX OPM – Adaptado) Na figura, vemos um quarto de círculo, com [tex]20 \, cm[/tex] de raio, e dois semicírculos internos a ele. Determinar a área da região colorida de verde.

Solução 1

---

Vamos fazer uma construção geométrica para ajudar na solução do problema:

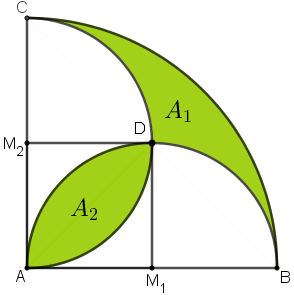
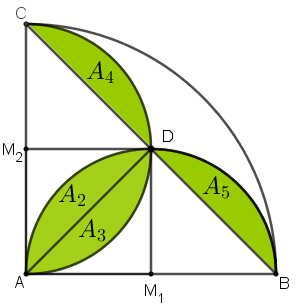
• considere o quadrado [tex] AM_1DM_2[/tex], construído a partir dos pontos médios [tex]M_1 \, [/tex] e [tex] \, M_2[/tex] dos diâmetros [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex], respectivamente, conforme mostra a próxima figura.

Devemos calcular a área da região colorida de verde, que denominaremos de [tex]A[/tex]. Para isso, calcularemos separadamente as áreas indicadas na figura como [tex]A_1 \, [/tex] e [tex] \, A_2.[/tex]

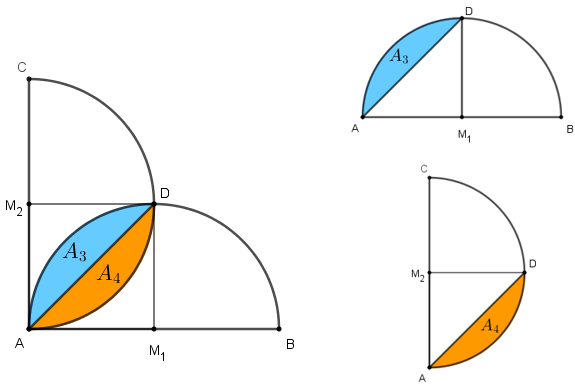
• Para calcularmos [tex]A_2[/tex], vamos observar apenas os semicírculos de diâmetros [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] e vamos dividir a região de área [tex]A_2[/tex] utilizando uma das diagonais do quadrado [tex] AM_1DM_2[/tex], conforme ilustrado na figura ao lado.

Observe que [tex]A_2=A_3+A_4[/tex] e que [tex]A_3=A_4[/tex].
Com efeito, perceba que:

• [tex]A_3[/tex] é a diferença entre a metade da área do semicírculo de diâmetro [tex]\overline{AB}[/tex] e a área do triângulo [tex]AM_1D;[/tex]
• [tex]A_4[/tex] é a diferença entre a metade da área do semicírculo de diâmetro [tex]\overline{AC}[/tex] e a área do triângulo [tex]AM_2D.[/tex]

Assim:
[tex]\qquad A_3=A_4=\dfrac{\frac{\pi 10^2}{2}}{2}-\dfrac{10 \times 10 }{2}
\\ \,
\qquad A_3=A_4=\dfrac{\pi 10^2}{2^2}- 10 \times 5
\\ \,
\qquad A_3=A_4=\left( 25 \pi- 50 \right) \, cm^2 \, ,[/tex]
donde segue que
[tex]\qquad A_2=A_3+A_4[/tex]
[tex]\qquad A_2=2 \times \left( 25 \pi- 50 \right)[/tex]
[tex]\qquad \fcolorbox{black}{#d7d7d7}{$A_2=\left( 50 \pi- 100 \right) \, cm^2$} \, .[/tex]



• Para calcularmos [tex]A_1[/tex], basta observar que essa área é a área de [tex]\frac{1}{4}[/tex] do círculo de raio [tex]\overline{AB}[/tex] menos três áreas: [tex]\frac{1}{4}[/tex] da área do círculo de raio [tex]\overline{AM_1}[/tex]; [tex]\frac{1}{4}[/tex] da área do círculo de raio [tex]\overline{AM_2}[/tex] e a área do quadrado [tex] AM_1DM_2[/tex], conforme ilustrado na figura ao lado.

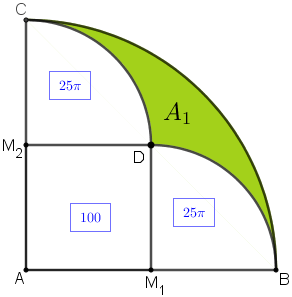
Dessa forma, temos que:
[tex]\qquad A_1=\dfrac{1}{4} \pi \, 20^2-\dfrac{1}{4} \pi \, 10^2-\dfrac{1}{4} \pi \, 10^2-10^2[/tex]
[tex]\qquad A_1=100 \pi -25 \pi -25 \pi -100[/tex]
[tex]\qquad \fcolorbox{black}{#d7d7d7}{$A_1=\left( 50 \pi- 100 \right) \, cm^2$} \, .[/tex]

Pronto, já podemos finalizar a nossa primeira solução e determinar a área [tex]A[/tex]:
[tex]\qquad A=A_1+A_2[/tex]
[tex]\qquad A=\left(50 \pi- 100 \right)+\left(50 \pi- 100 \right)[/tex]
[tex]\qquad A=\left(100 \pi- 200 \right) \, cm^2.[/tex]
Assim, a área da região colorida de verde mostrada na figura é [tex] \, \fcolorbox{black}{#eee0e5}{$\left(100 \pi- 200 \right) \, cm^2$} \, [/tex], ou seja, aproximadamente [tex] \, \fcolorbox{black}{#eee0e5}{$114 \, cm^2$} \, .[/tex]

---

Solução elaborada pelos Moderadores do Blog.

Solução 2

---

Nesta segunda solução, também construiremos o quadrado [tex] AM_1DM_2[/tex], a partir dos pontos médios [tex]M_1 \, [/tex] e [tex] \, M_2[/tex] dos diâmetros [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex], respectivamente.
Construído o quadrado, consideraremos as quatro regiões indicadas na próxima figura.

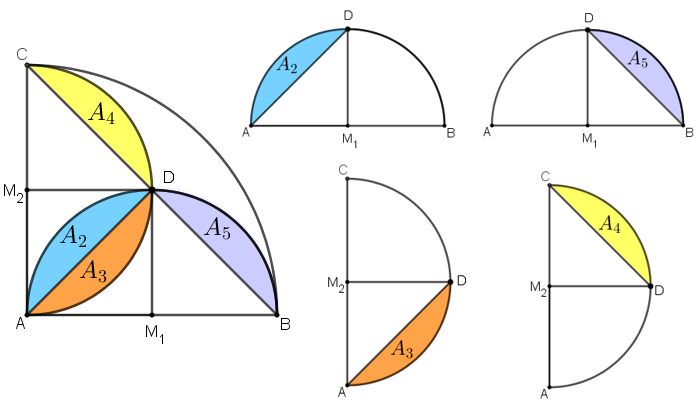
Observando apenas os semicírculos de diâmetros [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex], podemos perceber que essas quatro regiões são geometricamente equivalentes, ou seja, têm a mesma área:

• [tex]A_2[/tex] é a diferença entre a metade da área do semicírculo de diâmetro [tex]\overline{AB}[/tex] e a área do triângulo [tex]AM_1D;[/tex]
• [tex]A_3[/tex] é a diferença entre a metade da área do semicírculo de diâmetro [tex]\overline{AC}[/tex] e a área do triângulo [tex]AM_2D.[/tex]
• [tex]A_4[/tex] é a diferença entre a metade da área do semicírculo de diâmetro [tex]\overline{AC}[/tex] e a área do triângulo [tex]CM_2D;[/tex]
• [tex]A_5[/tex] é a diferença entre a metade da área do semicírculo de diâmetro [tex]\overline{AB}[/tex] e a área do triângulo [tex]BM_1D.[/tex]

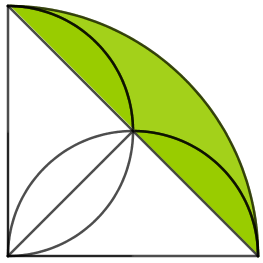
Dessa forma, a área verde da figura original é igual a área verde da figura abaixo, à qual denominaremos [tex]A_1.[/tex]

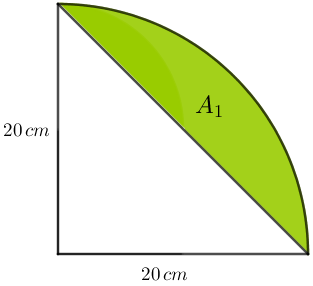
E observe como é simples calcular [tex]A_1[/tex], já que essa área é a diferença entre a área relativa a [tex]\frac{1}{4}[/tex] de um círculo de raio [tex]20[/tex] e a área de um triângulo retângulo com catetos [tex]20.[/tex]
Veja:
[tex]\qquad A_1=\dfrac{1}{4} \pi \, 20^2-\dfrac{20 \times 20}{2}\\
\, \, \\
\qquad A_1=100 \pi -200.\\
[/tex]
Assim, a área da região colorida de verde mostrada na figura é [tex] \, \fcolorbox{black}{#eee0e5}{$\left(100 \pi- 200 \right) \, cm^2$} \, [/tex], ou seja, aproximadamente [tex] \, \fcolorbox{black}{#eee0e5}{$114 \, cm^2$} \, .[/tex]

---

Solução elaborada pelos Moderadores do Blog.