✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Difícil)
Fixado um sistema ortogonal de eixos [tex]xOy[/tex], sabe-se que o ponto [tex]M=(2,1)[/tex] é ponto médio de uma corda [tex]\overline{AB}[/tex] da circunferência definida por
[tex]\qquad \qquad \quad \quad \qquad \qquad \boxed{ (x-1)^2+y^2=4}[/tex].
Qual a equação da reta que contém os pontos [tex]A[/tex] e [tex]B[/tex]?

Lembretes
(1) Ao representarmos uma reta [tex]r[/tex] em um plano cartesiano [tex]xOy[/tex], podemos associar equações a essa reta. Das várias formas de representarmos algebricamente [tex]r[/tex], duas são mais conhecidas:
Equação geral: equação do tipo [tex]\fcolorbox{black}{#E8E8E8}{$ ax+by+c=0$}[/tex] que é satisfeita por todos os pontos [tex]P=(x,y)[/tex] pertencentes a [tex]r.[/tex]
Equação reduzida: equação associada à reta [tex]r[/tex] e que é obtida da sua equação geral, [tex]ax+by+c=0[/tex], se [tex]b\ne 0.[/tex] Relembre:
[tex]ax+by+c=0 \Leftrightarrow by=-ax-c \stackrel{\textcolor{#800000}{b \ne 0}}{\Longrightarrow} y=\underbrace{\left(-\dfrac{a}{b}\right)}_{m}x+\underbrace{\left(-\dfrac{c}{b}\right)}_{n} \Longrightarrow \fcolorbox{black}{#E8E8E8}{$ y=mx+n $}[/tex]
Particularmente, o coeficiente [tex]m[/tex] é denominado o coeficiente angular e [tex]n[/tex] é o coeficiente linear da reta em questão. Geometricamente:
- A condição [tex]b\ne 0[/tex] significa que a reta [tex]r[/tex] não é vertical, ou seja, não é paralela ao eixo [tex]Oy.[/tex] Assim, retas não verticais têm as duas formas de equação: a geral e a reduzida.
- O coeficiente angular [tex]m[/tex] está associado ao declive da reta, isto é, ao ângulo que a reta define com o eixo horizontal [tex]Ox.[/tex]
- O coeficiente linear [tex]n[/tex] está associado ao ponto em que a reta intersecta o eixo [tex]Oy.[/tex]
(2) Duas retas não verticais são perpendiculares entre si se, e somente se, o produto de seus coeficientes angulares for [tex]-1.[/tex] Retas verticais distintas são sempre paralelas.
(3) Também podemos associar equações a uma circunferência [tex]c[/tex] representada em um plano cartesiano [tex]xOy[/tex]. Neste problema utilizaremos a chamada equação reduzida de [tex]c[/tex]:
[tex]\quad \quad \qquad\qquad \fcolorbox{black}{#E8E8E8}{$ \left(x-a\right)^2+ \left(y-b\right)^2=r^2$}[/tex]
que é satisfeita por todos os pontos [tex]P=(x,y)[/tex] pertencentes a [tex]c.[/tex]
Dois elementos importantes da circunferência [tex]c[/tex] aparecem explicitamente nessa equação:
- as coordenadas do centro da circunferência: [tex]C=(a,b)[/tex],
- o comprimento do raio da circunferência: [tex]r[/tex] .
(4) Caso de congruência L.L.L. (lado – lado – lado): Se dois triângulos têm ordenadamente congruentes os três lados, então estes triângulos são congruentes. (Se você não se lembra dos casos de congruência de triângulos, clique AQUI.)
Solução
Observe, inicialmente, que, de acordo com o Lembrete (3), o centro da circunferência dada no problema é o ponto [tex]C=(1,0)[/tex].
Vamos determinar a equação da reta [tex]r[/tex] que contém os pontos [tex]A[/tex] e [tex]B[/tex], a partir da reta [tex]s[/tex] determinada pelos pontos [tex]C=(1,0)[/tex] e [tex]M=(2,1)[/tex].
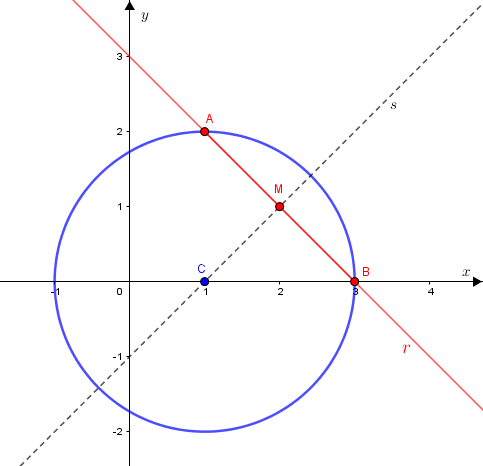
Vejamos, então, como obter a equação da reta [tex]s[/tex]:
- Como as primeiras coordenadas de [tex]C[/tex] e de [tex]M [/tex] são distintas ([tex]1 \ne 2[/tex]), a reta [tex]s[/tex] não é vertical e, portanto, [tex]s[/tex] tem equação reduzida:
[tex]\qquad y=m_sx+n_s. \qquad \textcolor{#800000}{(s)}[/tex] - Por outro lado, [tex]C[/tex] e [tex]M [/tex] são pontos de [tex]s[/tex]; assim, suas coordenadas satisfazem a equação de [tex]s[/tex]. Logo:
[tex]\qquad 0=m_s \cdot 1+n_s\\
\qquad 0=m_s+n_s \\
\qquad n_s=-m_s \qquad \textcolor{#800000}{(i)}\qquad \qquad [/tex] e [tex]\qquad \qquad 1=m_s \cdot 2+n_s \\
\qquad \qquad 1=2m_s+n_s. \qquad \textcolor{#800000}{(ii)}[/tex]
De [tex]\textcolor{#800000}{(i)}[/tex] e de [tex]\textcolor{#800000}{(ii)}[/tex], segue que:
[tex]\qquad 1=2m_s+n_s[/tex]
[tex]\qquad 1=2m_s-m_s[/tex]
[tex]\qquad m_s=1[/tex]
e, portanto, [tex]n_s=-1.[/tex]
Consequentemente, temos a equação reduzida de [tex]s[/tex]: [tex]\boxed{y=x-1}.[/tex]
Você pode estar se perguntando porque vamos utilizar a reta [tex]s[/tex]. A resposta é simples:
- As retas [tex]r[/tex] e [tex]s[/tex] são perpendiculares; logo, pelo Lembrete (2), já temos o coeficiente angular da reta [tex]r.[/tex] E como sabemos que [tex]M[/tex] é ponto de [tex]r[/tex], conseguimos a equação de [tex]r[/tex], sem muitos problemas.
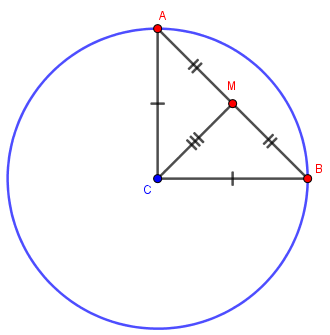
Dessa forma, precisamos mostrar que, de fato, [tex]r[/tex] e [tex]s[/tex] são perpendiculares. Para tanto observe a próxima figura, na qual destacamos a circunferência definida no problema, os pontos [tex]A,B,C,M[/tex] e os triângulos [tex]AMC[/tex] e [tex]BMC.[/tex]
Perceba que:
- Os segmentos [tex]\overline{CA}[/tex] e [tex]\overline{CB}[/tex] são raios da circunferência do problema, portanto têm a mesma medida.
- [tex]M[/tex] é ponto médio do segmento [tex]\overline{AB}[/tex], logo os segmentos [tex]\overline{AM}[/tex] e [tex]\overline{MB}[/tex] têm a mesma medida.
- O segmento [tex]\overline{CM}[/tex] é comum aos dois triângulos.
Desse modo, pelo Lembrete (4), os triângulos [tex]AMC[/tex] e [tex]BMC[/tex] são congruentes e, consequentemente, os ângulos [tex]A\hat{M}C[/tex] e [tex]B\hat{M}C[/tex] têm a mesma medida. Como esses ângulos são suplementares (a soma de suas medidas é [tex]180^{\circ}[/tex]), então cada ângulo mede [tex]90^{\circ}[/tex] e, com isso, os segmentos [tex]\overline{AM}[/tex] e [tex]\overline{CM}[/tex] (e consequentemente as retas [tex]s[/tex] e [tex]s[/tex]) são perpendiculares.
Pronto, já podemos determinar a equação da reta [tex]r[/tex]:
- Como [tex]s[/tex] não é uma reta horizontal e [tex]r[/tex] é perpendicular a [tex]s[/tex], então [tex]r[/tex] não é vertical e, portanto, tem equação reduzida:
[tex]\qquad y=m_rx+n_r. \qquad \textcolor{#800000}{(r)}[/tex] - Como [tex]s[/tex] e [tex]r[/tex] são perpendiculares, então, pelo Lembrete (2), [tex]m_r \cdot m_s=-1[/tex]. Da equação reduzida de [tex]s[/tex],[tex]\boxed{y=x-1}[/tex], obtemos que [tex]m_s=1[/tex], logo [tex]m_r =-1[/tex]. Dessa forma, podemos reescrever a equação reduzida de [tex]r[/tex]:
[tex]\qquad y=-x+n_r. \qquad \textcolor{#800000}{(r)}[/tex] - Sabemos que [tex]M=(2,1)[/tex] é um ponto de [tex]r[/tex]; assim, suas coordenadas satisfazem a equação de [tex]r[/tex]:
[tex]\qquad 1=-2+n_r \\
\qquad n_r=3.[/tex]
Deste modo, a equação reduzida da reta [tex]r[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$y=-x+3$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
