Linguagem matemática
Implicações e equivalências
Nas salas anteriores, vimos que equivalências são necessárias na substituição de uma frase por outra, sem que se perca o sentido lógico do discurso, e que implicações são extremamente úteis em processos dedutivos. Como sentenças abertas são utilizadas nos processos de generalização da Matemática e a Matemática é repleta de propriedades cujas validades são garantidas por demonstrações – os teoremas – é de se esperar que equivalências e implicações existam, também, entre sentenças abertas. É exatamente sobre isso que trataremos a partir de agora.
Para isso, utilizaremos uma linguagem menos lógica e mais matemática para ficarmos mais próximos do discurso que utilizamos no nosso contato diário com a Matemática. Assim, nesta sala falaremos de propriedades e não de sentenças abertas, embora propriedades matemáticas sejam sentenças abertas, quantificadas ou não, e utilizaremos a linguagem de conjuntos para sintetizar e organizar o nosso raciocínio, prática iniciada na Sala de enigmas 2. Toda a discussão sobre lógica elementar feita nas salas 1, 2 e 3 ajudará, e muito, no entendimento do que está por vir, já que nessas salas uma linguagem cotidiana logicamente correta nos foi apresentada.
Vamos lá?
Para efeito de notação, letras latinas maiúsculas, [tex]P[/tex], [tex]Q[/tex], [tex]R[/tex], [tex]\cdots[/tex], representarão propriedades que se referem a elementos genéricos de um dado conjunto não vazio [tex]U[/tex] (o conjunto universo do nosso discurso). Assim, por exemplo, podemos ter:
➤ [tex]U[/tex]: conjunto dos triângulos de um plano;
➤ [tex]P[/tex]: [tex]T[/tex] é equilátero;
➤ [tex]Q[/tex]: [tex]T[/tex] é isósceles.
➤ [tex]U[/tex]: conjunto dos números naturais;
➤ [tex]P[/tex]: [tex]a[/tex] é par;
➤ [tex]Q[/tex]: [tex]a[/tex] é múltiplo de [tex]5[/tex].
➤ [tex]U[/tex]: conjunto das retas de um plano;
➤ [tex]P[/tex]: [tex]r[/tex] e [tex]s[/tex] são paralelas;
➤ [tex]Q[/tex]: [tex]r[/tex] e [tex]s[/tex] são perpendiculares.
➤ [tex]U[/tex]: conjunto dos números racionais;
➤ [tex]P[/tex]: [tex]x^2 \in \mathbb{R}[/tex];
➤ [tex]Q[/tex]: [tex]\sqrt{x} \in \mathbb{R}[/tex].
Implicações
Se [tex]P[/tex] e [tex]Q[/tex] são propriedades que se referem a elementos de um dado conjunto não vazio [tex]U[/tex], então as cinco expressões:
- se [tex]P[/tex], então [tex]Q[/tex]
- [tex]P[/tex] implica [tex]Q[/tex]
- [tex]P[/tex] acarreta [tex]Q[/tex]
- [tex]P[/tex] é condição suficiente para [tex]Q[/tex]
- [tex]Q[/tex] é condição necessária para [tex]P[/tex]
têm todas o mesmo significado. Elas querem dizer, simplesmente, que:
- todo elemento do conjunto [tex]U[/tex] que tem a propriedade [tex]P[/tex] também tem a propriedade [tex]Q[/tex].
Para expressar esse fato, é comum utilizarmos a notação[tex] \, \, P \Rightarrow Q[/tex]; dessa forma, se considerarmos os conjuntos:
[tex] \, \, \, \, \, \, \, \, V_P=\{ \, p \in U[/tex], tal que [tex]p[/tex] tem a propriedade [tex]P \, \}[/tex]
[tex] \, \, \, \, \, \, \, \, V_Q=\{ \, q \in U[/tex], tal que [tex]q[/tex] tem a propriedade [tex]Q \, \}[/tex]
então escrevemos [tex] \, \, P \Rightarrow Q \, \, [/tex] para significar que [tex] \, \, V_P \subset V_Q[/tex].
Nessas condições, é comum também utilizarmos a notação [tex] \, \, P \nRightarrow Q[/tex] para indicar a negação de [tex] \, \, P \Rightarrow Q[/tex]; logo, a notação [tex] \, \, P \nRightarrow Q[/tex] indica que
- nem todo elemento do conjunto [tex]U[/tex] que tem a propriedade [tex]P[/tex] também tem a propriedade [tex]Q[/tex]
ou, de outra forma, indica que
- é possível encontrar, pelo menos, um elemento do conjunto [tex]U[/tex] que tenha a propriedade [tex]P[/tex] e que não tenha a propriedade [tex]Q[/tex].
Resumindo:
- [tex] \, \, P \Rightarrow Q \, [/tex]: todo elemento do conjunto [tex]U[/tex] que tenha a propriedade [tex]P[/tex] também tem a propriedade [tex]Q[/tex].
- [tex] \, \, P \nRightarrow Q \, [/tex]: é possível encontrar, pelo menos, um elemento do conjunto [tex]U[/tex] que tenha a propriedade [tex]P[/tex] e que não tenha a propriedade [tex]Q[/tex].
Generalizando:
Com efeito, sejam [tex]p(x)[/tex] e [tex]q(x)[/tex] sentenças abertas em um conjunto [tex]U[/tex] cujos conjuntos-verdade são [tex]V_p[/tex] e [tex]V_q[/tex], respectivamente.
Dizemos que [tex]p(x)[/tex] implica [tex]q(x)[/tex] se [tex]V_p \subset V_q[/tex]. Neste caso, podemos utilizar a notação [tex] \, \, p(x) \Rightarrow q(x) \, [/tex].
Equivalências
Se, novamente, [tex]P[/tex] e [tex]Q[/tex] forem propriedades que se referem a elementos de um dado conjunto não vazio [tex]U[/tex], também as expressões:
- [tex]P[/tex] é condição necessária e suficiente para [tex]Q[/tex]
- [tex]P[/tex] se, e somente se, [tex]Q[/tex]
- [tex]P[/tex] e [tex]Q[/tex] são equivalentes
têm todas o mesmo significado. Elas querem dizer que "[tex]P \Rightarrow Q[/tex]" e "[tex]Q \Rightarrow P[/tex]", ou seja, que, simultaneamente,
- “todo elemento do conjunto [tex]U[/tex] que tenha a propriedade [tex]P[/tex] também tem a propriedade [tex]Q[/tex]” e “todo elemento do conjunto [tex]U[/tex] que tenha a propriedade [tex]Q[/tex] também tem a propriedade [tex]P[/tex]”;
fato que denotamos como:[tex] \, \, P \Leftrightarrow Q[/tex]. Portanto, se considerarmos uma vez mais os conjuntos
[tex] \qquad V_P=\{ \, p \in U[/tex], tal que [tex]p[/tex] tenha a propriedade [tex]P \, \}[/tex]
[tex] \qquad V_Q=\{ \, q \in U[/tex], tal que [tex]q[/tex] tenha a propriedade [tex]Q \, \}[/tex]
então escrever [tex] \, \, P \Leftrightarrow Q \, \, [/tex] significa que [tex] \, \, V_P = V_Q \, \, [/tex].
Também é comum utilizarmos uma notação para indicar a negação de [tex] \, \, P \Leftrightarrow Q[/tex]. Assim, a notação [tex] \, \, P \nLeftrightarrow Q[/tex] indica que [tex]P[/tex] e [tex]Q[/tex] não são equivalentes, ou seja, que, pelo menos, uma das seguintes situações ocorre: [tex] \, \, P \nRightarrow Q[/tex]; [tex] \, \, Q \nRightarrow P[/tex].
Resumindo:
- [tex] \, \, P \Leftrightarrow Q \, [/tex]: [tex] \, \, P \Rightarrow Q \, [/tex] e [tex] \, \, Q \Rightarrow P \, [/tex];
- [tex] \, \, P \nLeftrightarrow Q \, [/tex]: [tex] \, \, P \nRightarrow Q \, [/tex] ou [tex] \, \, Q \nRightarrow P \, [/tex].
Generalizando:
Assim, se [tex]p(x)[/tex] e [tex]q(x)[/tex] são sentenças abertas em um conjunto [tex]U[/tex] cujos conjuntos-verdade são [tex]V_p[/tex] e [tex]V_q[/tex], respectivamente, dizemos que [tex]p(x)[/tex] e [tex]q(x)[/tex] são equivalentes se [tex]V_p = V_q[/tex]. Neste caso, podemos utilizar a notação [tex] \, \, p(x) \Leftrightarrow q(x) \, [/tex].
As expressões “se, então” e “se, e somente se” utilizadas relacionando propriedades genéricas são de extrema importância para a leitura e compreensão de textos de Matemática; portanto, vamos resumir e registrar suas características.

Já que uma equivalência nada mais é do que uma dupla implicação, vamos centrar nossas discussões nas implicações.
Observamos, inicialmente, que quando afirmamos que "[tex] \, P \Rightarrow Q \, [/tex] significa que [tex] \, V_P \subset V_Q[/tex]", não estamos afirmando que, para mostrar que uma propriedade [tex]P[/tex] implica uma propriedade [tex]Q[/tex], vamos necessariamente construir os conjuntos [tex]V_P[/tex] e [tex]V_Q[/tex] e verificar que [tex]V_P \subset V_Q[/tex]. Embora isso seja possível em algumas situações muito particulares, as sentenças abertas da Matemática e, portanto, as propriedades matemáticas, são definidas frequentemente em conjuntos que não permitem esse tipo de construção prática. (Como construiríamos, na prática, o conjunto de todos os triângulos isósceles de um plano, ou o conjunto de todas as retas [tex]a, \, b, \, c[/tex] de um plano tais que [tex]a \parallel b[/tex] e [tex]b\parallel c[/tex]?)
A maneira matemática de se verificar que [tex] \, P \Rightarrow Q \, [/tex] é quase sempre por meio de uma demonstração na qual, a partir da ocorrência da propriedade [tex]P[/tex], é possível deduzir a ocorrência de [tex]Q[/tex] por meio de uma sequência de argumentações válidas dentro da teoria onde a implicação foi enunciada. Assim, as demonstrações são o "como garantir, sustentar, validar uma implicação" e claramente dependem da teoria do Universo no qual as propriedades envolvidas estão definidas; mas o entendimento e a manipulação lógica das implicações (e das equivalências) entre propriedades matemáticas podem ser traduzidos em termos de noções e propriedades sobre conjuntos, desde que sustentadas por uma linguagem cotidiana logicamente correta. E é isso que passaremos a fazer a seguir.
Resultados importantes
Sejam [tex]U[/tex] um conjunto não vazio, [tex]P, \, Q, \, S[/tex] propriedades relativas a elementos de [tex]U[/tex] e os seguintes subconjuntos de [tex]U[/tex]:
[tex] \qquad V_P=\{ \, p \in U[/tex], tal que [tex]p[/tex] tenha a propriedade [tex]P \, \}[/tex]
[tex] \qquad V_Q=\{ \, q \in U[/tex], tal que [tex]q[/tex] tenha a propriedade [tex]Q \, \}[/tex]
[tex] \qquad V_S=\{ \, s \in U[/tex], tal que [tex]s[/tex] tenha a propriedade [tex]R \, \}[/tex]
✐ Uma das propriedades sobre conjuntos nos garante que se [tex]A, \, B, \, D[/tex] são conjuntos tais que [tex]\boxed{A \subset B}[/tex] e [tex]\boxed{B \subset D}[/tex], então [tex]\boxed{A \subset D}[/tex].
Considerando as propriedades [tex]P, \, Q, \, S[/tex], se os conjuntos [tex]V_P[/tex], [tex]V_Q[/tex] e [tex]V_S[/tex] são tais que [tex]V_P \subset V_Q[/tex] e [tex]V_Q \subset V_S[/tex], então [tex]V_P \subset V_S[/tex].
Dessa forma, temos a seguinte propriedade sobre implicação:
Se [tex]P \Rightarrow Q \, [/tex] e [tex] \, Q \Rightarrow S[/tex], então [tex]P \Rightarrow S[/tex].
Essa propriedade é conhecida como transitividade da implicação.
✐ A transitividade da igualdade entre conjuntos nos garante que se [tex]A, \, B, \, D[/tex] são conjuntos tais que [tex]\boxed{A = B}[/tex] e [tex]\boxed{B = D}[/tex], então [tex]\boxed{A = D}[/tex].
Considerando mais uma vez as propriedades [tex]P, \, Q, \, S[/tex], se os conjuntos [tex]V_P[/tex], [tex]V_Q[/tex] e [tex]V_S[/tex] são tais que [tex]V_P = V_Q[/tex] e [tex]V_Q = V_S[/tex], então [tex]V_P = V_S[/tex].
Dessa forma, temos a seguinte propriedade sobre equivalência:
Se [tex]P \Leftrightarrow Q \, [/tex] e [tex] \, Q \Leftrightarrow S[/tex], então [tex]P \Leftrightarrow S[/tex].
Essa propriedade é conhecida como transitividade da equivalência.
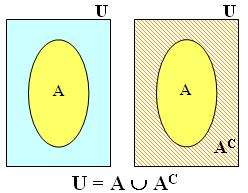
✐ Seja [tex]A[/tex] um subconjunto não vazio de [tex]U[/tex].
Assim, dado um elemento [tex]u[/tex] de [tex]U[/tex] temos duas alternativas mutuamente excludentes: ou [tex]u \in A[/tex] ou [tex]u \not \in A[/tex].
Os elementos de [tex]U[/tex] que não são elementos de [tex]A[/tex] definem o conjunto denotado por [tex]A^C[/tex] e denominado o complementar de [tex]A[/tex] com relação a [tex]U[/tex]:
[tex]\qquad A^C=\{u \in U \, | \, u \not \in A\}[/tex].
Olhando, então, a propriedade [tex]P[/tex], observamos que [tex]\left(V_P\right)^C[/tex] é o conjunto dos elementos de [tex]U[/tex] que não pertencem a [tex]V_P[/tex], ou seja, o conjunto dos elementos de [tex]U[/tex] que não têm a propriedade [tex]P[/tex].
Dessa forma, podemos afirmar que:
A propriedade que caracteriza os elementos do conjunto [tex]\left(V_P\right)^C \, [/tex] é a negação de [tex]P[/tex], isto é, "não [tex]P[/tex]". Em analogia às sentenças abertas, denotaremos a propriedade "não [tex]P[/tex]" por "[tex]\sim P[/tex]".
✐ Uma propriedade não trivial de conjuntos garante que se [tex]A, \, B[/tex] são subconjuntos de [tex]U[/tex] tais [tex]\boxed{A \subset B}[/tex], então [tex]\boxed{B^C \subset A^C}[/tex], onde [tex]A^C[/tex] e [tex]B^C[/tex] são, respectivamente, os complementares de [tex]A[/tex] e de [tex]B[/tex] com relação a [tex]U[/tex].
A figura abaixo ilustra essa propriedade.
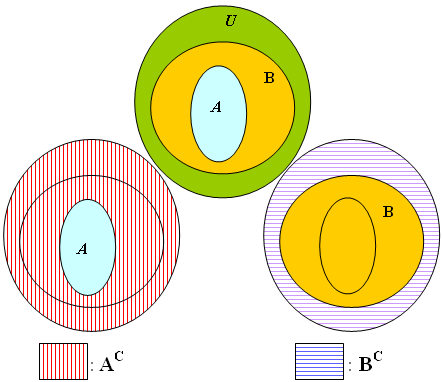
Assim, se os conjuntos [tex]V_P[/tex] e [tex]V_Q[/tex] são tais que [tex]V_P \subset V_Q[/tex], então [tex]\left(V_Q\right)^C \subset \left(V_P\right)^C[/tex] e com isso garantimos que
- se "[tex]P \Rightarrow Q \, [/tex]", então "[tex]\sim Q \Rightarrow \sim P[/tex]". [tex]\qquad (i)[/tex]
Mas podemos ir além se utilizarmos mais uma propriedade envolvendo complementares; observe.
✐ Se [tex]A[/tex] é um subconjunto de [tex]U[/tex], então o complementar do complementar de [tex]A[/tex] é o próprio [tex]A[/tex]: [tex]\boxed{\left(A^C\right)^C=A}[/tex].
A partir dessa última propriedade, podemos afirmar que "se [tex]\left(V_Q\right)^C \subset \left(V_P\right)^C[/tex], então [tex]\left(\left(V_P\right)^C\right)^C \subset \left(\left(V_Q\right)^C\right)^C[/tex]", isto é, "se [tex]\left(V_Q\right)^C \subset \left(V_P\right)^C[/tex], então [tex]V_P \subset V_Q[/tex]". Com isso garantimos, agora, que
- se "[tex]\sim Q \Rightarrow \sim P[/tex]", então "[tex]P \Rightarrow Q \, [/tex]".[tex]\qquad (ii)[/tex]
Por [tex](i)[/tex] e [tex](ii)[/tex], segue que
"[tex]P \Rightarrow Q \, [/tex]" se, e somente se, "[tex]\sim Q \Rightarrow \sim P[/tex] ".
Reconheceu a propriedade? É isso mesmo, também para as propriedades (e, em geral, para as sentenças abertas), temos a propriedade que garante que uma implicação e sua contrapositiva são equivalentes.
Lá na Sala 1, observamos que o “se …, então …” e o "se, e somente se " que alguns estavam esperando não eram os lá definidos. Pois bem, o "se, então" e o "se, e somente se" que utilizamos nos enunciados da Matemática são os aqui apresentados.
Nestes casos, utilizamos a notação [tex] \, P \Rightarrow Q \, [/tex] e a frase "Se [tex]P[/tex], então [tex]Q[/tex]" é dita uma implicação lógica ou, simplesmente, uma implicação. A lousinha lá em cima mostra outras formas de leitura da notação [tex] \, P \Rightarrow Q \, [/tex].
É comum também se afirmar que a implicação [tex] \, Q \Rightarrow P \, [/tex] é a recíproca da implicação [tex] \, P \Rightarrow Q \, [/tex].
Observamos que o símbolo [tex] \, \Rightarrow \, [/tex] não denota a palavra portanto, nem a palavra então. Ele deve ser utilizado com o significado de implica, quando aparece ligando duas sentenças abertas (em particular, ligando duas propriedades matemáticas). Assim, não escreva frases do tipo
"Todo múltiplo de quatro é múltiplo de dois. [tex]16[/tex] é múltiplo de [tex]4 \Rightarrow 16[/tex] é múltiplo de [tex]2[/tex]."
ou
" Se [tex]x \in \{2, \, 5\} \Rightarrow x^2-7x+10=0[/tex]. "!
Nestes casos, utilizamos a notação [tex] \, P \Leftrightarrow Q \, [/tex] e a frase "[tex]P[/tex] se, e somente se, [tex]Q[/tex]" é dita uma equivalência lógica ou, simplesmente, uma equivalência. A lousinha lá em cima também mostra outras formas de leitura da notação [tex] \, P \Leftrightarrow Q \, [/tex].
Podemos ter uma sequência de propriedades (sentenças abertas), uma equivalente à outra:
[tex]\qquad \qquad \, P_1 \Leftrightarrow P_2 \Leftrightarrow P_3 \Leftrightarrow \dots \Leftrightarrow P_n[/tex]
e, neste caso, diremos apenas que as propriedades (sentenças) [tex] \, P_1, \, P_2, \dots, \, P_n \, [/tex] são equivalentes.
Observamos que o símbolo [tex] \, \Leftrightarrow \, [/tex] não deve ser utilizado em substituição ao símbolo [tex] \, = \, [/tex], pois ele não denota igualdade. Percebam que uma característica da igualdade é que todo objeto é igual a si próprio, e somente a si próprio e esta não é uma característica da equivalência!

Equipe COM – OBMEP
