A linguagem matemática
As frases matemáticas
Na linguagem cotidiana, chamamos de frase a todo enunciado de sentido completo; assim, uma frase pode ser formada por uma só palavra ou por várias. Elas podem, inclusive, não ter verbos, como esta: “Que dia lindo!”. De acordo com o sentido que transmitem, as frases podem ser classificadas como declarativas, interrogativas, exclamativas, imperativas, entre outras. Uma frase que tenha verbo (ou uma locução verbal) é chamada de oração.
A Matemática tem particular interesse em um tipo de frase: as chamadas proposições.
Proposições e conectivos
[tex]\textcolor{#996b0e}{(i)}[/tex] Princípio do terceiro excluído: Uma proposição é falsa ou verdadeira, excluindo-se uma terceira possibilidade.
[tex]\textcolor{#996b0e}{(ii)}[/tex] Princípio da não contradição: Uma proposição não pode ser verdadeira e falsa ao mesmo tempo.
Proposições podem ser indicadas por letras latinas minúsculas, indexadas ou não, tais como [tex]p\, ,\, q\,,\, r\,, \, p_1\,,\,p_2\,,\,p_3\,,\, q_1\,,\,q_2\,,\,q_3[/tex].
Observamos que dizer que uma proposição "pode ser classificada como verdadeira ou falsa" não significa que "saibamos classificá-la como verdadeira ou falsa". Por exemplo, a oração
Pidhaitsi é uma cidade da China.
é uma proposição, embora nenhum de nós seja capaz de dizer, neste momento, se ela é uma proposição verdadeira ou falsa. Procurando em um site de busca, podemos verificar que a proposição é falsa, pois Pidhaitsi é uma cidade da Ucrânia. A oração
O algarismo que aparece na posição 1 345 678 274
da representação decimal do número [tex]\pi[/tex] é o 3.
também é uma proposição, embora nenhum de nós seja capaz de dizer neste momento (e nem daqui a pouco) se ela é uma proposição verdadeira ou falsa.
Exemplos e contraexemplos:
Observem as frases abaixo.
(6) [tex]5 \times 3=15[/tex]?
(7) João e Maria
(8) [tex]2+9[/tex]
(2) Nossa, que frio!
(3) [tex]2+3=7[/tex]
(4) Brasília é a capital do Brasil.
A frase (1) é uma proposição verdadeira.
A frase (2) não é uma proposição, pois não é uma oração declarativa: ela é exclamativa e nem mesmo é uma oração, pois não tem verbo.
A frase (3) é uma proposição falsa.
A frase (4) é uma proposição verdadeira.
A frase (5) não é uma proposição, já que não pode ser classificada como verdadeira ou falsa, pois não se sabe o valor de [tex]x[/tex].
A frase (6) não é uma proposição, pois não é uma oração declarativa. (Ela é interrogativa)
Os exemplos (7) e (8) não são proposições, pois sequer são frases, já que nenhum tem sentido completo.
As três proposições poderiam ser indicadas por letras:
[tex]\qquad p: 2 \gt 1[/tex],
[tex]\qquad q: 2+3=7[/tex],
[tex]\qquad r:[/tex] Brasília é a capital do Brasil.
Proposições que não envolvam objetos ou símbolos matemáticos, como a do primeiro exemplo e a proposição (4), não vão nos interessar (embora interessem à Lógica); assim, daqui para frente, teremos a preferência de ilustrar nossas discussões sobre proposições com exemplos, digamos, matemáticos.
De modo geral, as proposições podem ser de dois tipos:
➤ proposições simples: aquelas que não contêm outra proposição como parte de si mesma. Assim, são caracterizadas por apresentarem apenas uma ideia;
➤ proposições compostas: aquelas que são formadas pela combinação de outras proposições.
Podemos construir novas proposições, a partir de outras dadas, utilizando, basicamente, cinco expressões/palavras especiais – os chamados conectivos. São eles:
➤ "não", simbolizado por [tex]\sim[/tex];
➤ "e", simbolizado por [tex]\land[/tex];
➤ "ou", simbolizado por [tex]\lor[/tex];
➤ "se …, então …", simbolizado por [tex]\rightarrow[/tex];
➤ "… se e somente se …", simbolizado por [tex]\longleftrightarrow[/tex].
Vejamos o comportamento de cada conectivo e como classificar como verdadeiras (V) ou falsas (F) proposições que são construídas a partir deles. Essa nossa breve discussão sobre os conectivos faz parte de um importante tópico da Lógica chamado Cálculo Proposicional.
Chamamos de negação de [tex]p[/tex] a proposição "não [tex]p[/tex]", que pode ser denotada por [tex]\sim p[/tex].
Por exemplo:
[tex] \, \, \, \, r[/tex]: [tex]2+2=9[/tex] ([tex]2+2[/tex] é igual a [tex]9[/tex]),
[tex]\sim r[/tex]: [tex]2+2\ne 9[/tex] ([tex]2+2[/tex] não é igual [tex]9[/tex] ou [tex]2+2[/tex] é diferente de [tex]9[/tex]).
[tex] \, \, \, \, s[/tex]: [tex]2[/tex] é um número par,
[tex]\sim s[/tex]: [tex]2[/tex] não é um número par.
De forma geral, se [tex]p[/tex] é uma proposição, a relação entre a verdade ou falsidade de [tex]p[/tex] e [tex]\sim p[/tex] é assim definida:
[tex]\begin{array}{c|c}
p &\sim p\\
\hline
V&F\\
F&V\\
\end{array}[/tex]
|
✐Exemplo: A proposição [tex]\quad \sim r: \, 2+2\ne 9[/tex] é verdadeira, pois a proposição [tex]\quad r: \, 2+2=9[/tex] é falsa. |
✐Exemplo: A proposição [tex]\quad \sim s[/tex]: [tex]2[/tex] não é um número par é falsa, pois a proposição [tex]\quad s[/tex]: [tex]2[/tex] é um número par é verdadeira. |
Chamamos de conjunção de [tex]p[/tex] e [tex]q[/tex] a proposição "[tex]p[/tex] e [tex]q[/tex] ", que pode ser denotada por [tex]p \land q[/tex].
Por exemplo:
[tex]a[/tex]: [tex]2[/tex] é primo,
[tex]b[/tex]: [tex]3 \times 3=7[/tex],
[tex]a \land b[/tex]: [tex]2[/tex] é primo e [tex]3 \times 3=7[/tex].
[tex]r[/tex]: [tex]2+1=3[/tex],
[tex]s[/tex]: [tex]4[/tex] é ímpar,
[tex]r \land \sim s[/tex]: [tex]2+1=3[/tex] e [tex]4[/tex] não é ímpar.
De forma geral, se [tex]p[/tex] e [tex]q[/tex] são proposições, a relação entre a verdade ou falsidade de [tex]p[/tex], [tex]q[/tex] e [tex]p \land q[/tex] é assim definida:
[tex]\begin{array}{cc|c}
p & q & p\land q\\
\hline
V&V&V\\
V&F&F\\
F&V&F\\
F&F&F\\
\end{array}[/tex]
|
✐Exemplo: A proposição [tex]\quad a \land b[/tex]: [tex]2[/tex] é primo e [tex]3 \times 3=7[/tex] é falsa, pois a proposição [tex]\quad a[/tex]: [tex]2[/tex] é primo, é verdadeira, mas a proposição [tex]\quad b[/tex]: [tex]3 \times 3=7[/tex], é falsa. |
✐Exemplo: A proposição [tex]\quad r \land \sim s[/tex]: [tex]2+1=3[/tex] e [tex]4[/tex] não é ímpar é verdadeira, pois a proposição [tex]\quad r[/tex]: [tex]2+1=3[/tex] é verdadeira e a proposição [tex]\quad \sim s[/tex]: [tex]4[/tex] não é ímpar, também é verdadeira. |
Chamamos de disjunção de [tex]p[/tex] e [tex]q[/tex] a proposição "[tex]p[/tex] ou [tex]q[/tex] ", que pode ser denotada por [tex]p \lor q[/tex].
Por exemplo:
[tex] a[/tex]: [tex]2^3=8[/tex],
[tex] b[/tex]: [tex]123[/tex] é par,
[tex] a \lor b[/tex]: [tex]2^3=8[/tex] ou [tex]123[/tex] é par.
[tex] r[/tex]: [tex]11[/tex] é primo,
[tex]s [/tex]: [tex]9[/tex] é ímpar,
[tex]r \lor s[/tex]: [tex]11[/tex] é primo ou [tex]9[/tex] é ímpar.
De forma geral, se [tex]p[/tex] e [tex]q[/tex] são proposições, a relação entre a verdade ou falsidade de [tex]p[/tex], [tex]q[/tex] e [tex]p \lor q[/tex] é assim definida:
[tex]\begin{array}{cc|c}
p & q & p\lor q\\
\hline
V&V&V\\
V&F&V\\
F&V&V\\
F&F&F\\
\end{array}[/tex]
Ou Maria ou João sentará nesta cadeira. (Aqui temos duas opções: "Maria senta e João não senta"; "João senta e Maria não senta".)
O "ou" da matemática tem o mesmo significado do "ou" simples do português:
Maria ou João entrarão nessa sala. (Aqui temos três opções: "Maria entra e João não entra"; "João entra e Maria não entra"; "João e Maria entram".)
Fazemos esta observação, pois muitas pessoas utilizam no português o "ou" simples, sem a devida repetição, para expressar a ideia de exclusão.
|
✐Exemplo: A proposição [tex]\quad a \lor b[/tex]: [tex]2^3=8[/tex] ou [tex]123[/tex] é par é verdadeira, pois a proposição [tex]\quad a[/tex]: [tex]2^3=8[/tex] é verdadeira, mesmo sendo a proposição [tex]\quad b[/tex]: [tex]123[/tex] é par falsa. |
✐Exemplo: A proposição [tex]\quad r \lor s[/tex]: [tex]11[/tex] é primo ou [tex]9[/tex] é ímpar é verdadeira, pois a proposição [tex]\quad r[/tex]: [tex]11[/tex] é primo é verdadeira e a proposição [tex]\quad s [/tex]: [tex]9[/tex] é ímpar também é verdadeira. |
Chamamos de condicional de [tex]p[/tex] e [tex]q[/tex], nesta ordem, a proposição " se [tex]p[/tex], então [tex]q[/tex] ", que pode ser denotada por [tex]p \rightarrow q[/tex].
Por exemplo:
[tex]p[/tex]: [tex]3 [/tex] é par,
[tex]q[/tex]: [tex]\sqrt{4}=5[/tex],
[tex]p \rightarrow q[/tex]: se [tex]3 [/tex] é par, então [tex]\sqrt{4}=5[/tex].
[tex]p[/tex]: [tex]\pi[/tex] é irracional,
[tex]q[/tex]: [tex]1+1=2[/tex],
[tex]p \rightarrow q[/tex]: se [tex]\pi[/tex] é irracional, então [tex]1+1=2[/tex].
De forma geral, se [tex]p[/tex] e [tex]q[/tex] são proposições, a relação entre a verdade ou falsidade de [tex]p[/tex], [tex]q[/tex] e [tex]p \rightarrow q[/tex] é assim definida:
[tex]\begin{array}{cc|c}
p & q & p\rightarrow q\\
\hline
V&V&V\\
V&F&F\\
F&V&V\\
F&F&V\\
\end{array}[/tex]
|
✐Exemplo: A proposição [tex]\quad p \rightarrow q[/tex]: se [tex]3 [/tex] é par, então [tex]\sqrt{4}=5[/tex] é verdadeira, pois a proposição [tex]\quad p[/tex]: [tex]3 [/tex] é par é falsa e a proposição [tex]\quad q[/tex]: [tex]\sqrt{4}=5[/tex] também é falsa. |
✐Exemplo: A proposição [tex]\quad p \rightarrow q[/tex]: se [tex]\pi[/tex] é irracional, então [tex]1+1=2[/tex] é verdadeira, pois a proposição [tex]\quad p[/tex]: [tex]\pi[/tex] é irracional é verdadeira e a proposição [tex]\quad q[/tex]: [tex]1+1=2[/tex] também é verdadeira. |
Pois é, elas são proposições, sim. E proposições verdadeiras!
Perceba que na definição não está sendo exigido que as proposições que definem uma condicional tenham alguma relação.
Informamos que o "se …, então …" que alguns estavam esperando não é esse…
 Estranhou de novo?
Estranhou de novo?Então responda:
Qual o nome da fruta que aparece na figura ao lado?
Qual é o nome da parte da camisa para a qual está apontada a seta?
Entendeu, não é?
Então aguarde pelo outro "se …, então …".
Esse outro "se …, então …" é mais utilizado na linguagem matemática, mas ele depende deste "se …, então …" que acabamos de definir.
Chamamos de bicondicional de [tex]p[/tex] e [tex]q[/tex] a proposição " [tex]p[/tex] se e somente se [tex]q[/tex] ", que pode ser denotada por [tex]p \longleftrightarrow q[/tex].
Por exemplo:
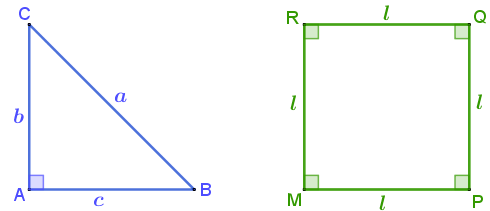
[tex]p[/tex]: O triângulo [tex]ABC[/tex] é retângulo,
[tex]q[/tex]: O quadrilátero [tex]MPQR[/tex] é um quadrado,
[tex]p \longleftrightarrow q[/tex]: O triângulo [tex]ABC[/tex] é retângulo se e somente se o quadrilátero [tex]MPQR[/tex] é um quadrado.
[tex]p[/tex]: [tex]2 \times 4=23[/tex],
[tex]q[/tex]: [tex]\sqrt{2}[/tex] é um número natural,
[tex]p \longleftrightarrow q[/tex]: [tex]2 \times 4=23[/tex] se e somente se [tex]\sqrt{2}[/tex] é um número natural.
De forma geral, se [tex]p[/tex] e [tex]q[/tex] são proposições, a relação entre a verdade ou falsidade de [tex]p[/tex], [tex]q[/tex] e [tex]p \longleftrightarrow q[/tex] é assim definida:
[tex]\begin{array}{cc|c}
p & q & p\longleftrightarrow q\\
\hline
V&V&V\\
V&F&F\\
F&V&F\\
F&F&V\\
\end{array}[/tex]
|
✐Exemplo: A proposição [tex]\quad p \longleftrightarrow q[/tex]: O triângulo [tex]ABC[/tex] é retângulo se e somente se o quadrilátero [tex]MPQR[/tex] é um quadrado é verdadeira, pois a proposição [tex]\quad p[/tex]: O triângulo [tex]ABC[/tex] é retângulo é verdadeira e a proposição [tex]q[/tex]: O quadrilátero [tex]MPQR[/tex] é um quadrado também é verdadeira . |
✐Exemplo: A proposição [tex]\quad p \longleftrightarrow q[/tex]: [tex]2 \times 4=23[/tex] se e somente se [tex]\sqrt{2}[/tex] é um número natural é verdadeira, pois a proposição [tex]\quad p[/tex]: [tex]2 \times 4=23[/tex] é falsa e a proposição [tex]\quad q[/tex]: [tex]\sqrt{2}[/tex] é um número natural também é falsa. |
Observe que também na definição de uma proposição bicondicional não está sendo exigido que as proposições que a definem tenham alguma relação.
Em breve apresentaremos o "se, e somente se" aguardado por muitos.
Interpretando e escrevendo melhor!
Pelo até aqui exposto, a partir de proposições [tex]p[/tex] e [tex]q[/tex] podemos definir novas proposições utilizando os conectivos
[tex]\qquad \qquad\textcolor{#996b0e}{\sim}[/tex] [tex]\qquad \qquad\textcolor{#996b0e}{\land}[/tex] [tex]\qquad \qquad \textcolor{#996b0e}{\lor}[/tex] [tex]\qquad \qquad \textcolor{#996b0e}{\rightarrow}[/tex] [tex]\qquad \qquad \textcolor{#996b0e}{\longleftrightarrow}[/tex]
e a verdade ou falsidade dessas novas proposições ficam definidas de maneira única a partir da verdade ou falsidade das proposições [tex]p[/tex] e [tex]q[/tex], de acordo com a seguinte tabela geral:
[tex]\begin{array}{cc|c|c|c|c|c}
p & q &\sim p&p \land q & p \lor q & p \rightarrow q & p\longleftrightarrow q\\
\hline
V&V&F&V&V&V&V\\
V&F&F&F&V&F&F\\
F&V&V&F&V&V&F\\
F&F&V&F&F&V&V\\
\end{array}[/tex]
Mas como escrever e interpretar uma proposição definida por mais de um conectivo?
Isso é feito com base em apenas duas convenções. A seguir, veremos como.
Assim, por exemplo, a proposição composta
[tex]\qquad (2+3=5 \land 8 \times 1=8) \rightarrow 2 \, [/tex] é par
é uma condicional, enquanto que a proposição
[tex]\qquad 2+3=5 \land (8 \times 1=8 \rightarrow 2 \,)[/tex] é par
é uma conjunção.
Portanto, uma proposição composta da forma [tex]\boxed{\sim q \rightarrow p}[/tex], por exemplo, é uma condicional, já que o conectivo [tex]\sim [/tex] tem precedência sobre o conectivo [tex]\rightarrow [/tex].
Para torná-la uma negação, teríamos que enfraquecer o conectivo [tex]\rightarrow [/tex] utilizando parêntesis:[tex]\boxed{\sim \left(q \rightarrow p\right)}.[/tex]
Exercícios
1) Determine se as seguintes proposições são verdadeiras ou falsas:
a) [tex] 5 \gt 2[/tex] e [tex]5 = 2[/tex]
b) [tex] 5 \gt 2[/tex] ou [tex]5 = 2[/tex]
c) [tex] 5 \ge 2[/tex]
d) [tex] 5 \le 2[/tex]
e) [tex]2[/tex] é par e é primo
f) [tex]\sqrt{2}[/tex] é racional ou [tex]\sqrt{2}[/tex] é irracional.
g) [tex]\sqrt{2}[/tex] é racional e [tex]\sqrt{2}[/tex] é irracional.
2) Dadas proposições [tex]p[/tex], [tex]q[/tex], e [tex]r[/tex] tais que [tex]q[/tex] é verdadeira e [tex]r[/tex] é falsa, o que podemos dizer sobre a verdade ou falsidade das proposições a seguir?
a) [tex]p \land q \, \, \qquad[/tex] b) [tex]p \lor q \, \, \qquad[/tex] c) [tex]q \rightarrow p \, \, \qquad[/tex] d) [tex]r \rightarrow q \, \, \qquad[/tex] e) [tex]r \rightarrow p \, \, \qquad[/tex] f) [tex]p \rightarrow r \, \, \qquad[/tex] g) [tex](r \rightarrow q) \lor p \, \, \qquad[/tex]
h) [tex]p \longleftrightarrow q\qquad[/tex] i) [tex]\sim (r \rightarrow q )\qquad[/tex] j) [tex]\sim r \rightarrow q\qquad[/tex] k) [tex]p\, \lor \sim p\qquad[/tex] l) [tex]p \lor p\qquad[/tex] m) [tex]q \rightarrow q\qquad[/tex] n) [tex]r \longleftrightarrow r \qquad[/tex]
Equipe COM – OBMEP
