Seja [tex]A[/tex] um conjunto não vazio.
Uma partição de um conjunto [tex]A[/tex] é qualquer coleção [tex]C[/tex] de subconjuntos não vazios de [tex]A[/tex] dotada da seguinte propriedade:
todo elemento de [tex]A[/tex] pertence a um e apenas um dos elementos de [tex]C[/tex].
Assim uma coleção de conjuntos [tex]C=\{A_1, A_2, \, \cdots \, , A_n\}[/tex] é uma partição (finita) do conjunto [tex]A[/tex], se as seguintes condições forem simultaneamente satisfeitas:
(1) [tex]A_i\ne\emptyset[/tex], para [tex]i=1, \, 2, \, \cdots \, ,n[/tex];
(2) [tex]A_i\subset A[/tex], para [tex]i=1, \, 2, \, \cdots \, ,n[/tex];
(3) [tex]A = A_1 \cup A_2 \cup \cdots \cup A_n [/tex];
(4) [tex] A_1, \, A_2 , \, \cdots , \, A_n [/tex] são mutuamente disjuntos, isto é, [tex] A_i \cap A_j =\emptyset[/tex], para [tex]i\ne j[/tex], com [tex]i,j=1, \, 2, \, \cdots \, ,n[/tex].
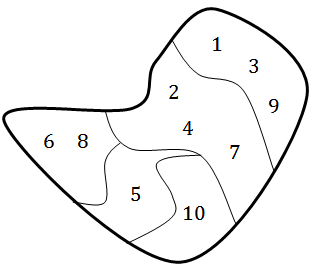 Exemplo:
Exemplo:
Se
[tex] X=\{1,2,3,4,5,6,7,8,9,10\}[/tex],
então
[tex] C=\{\{1,3,9\},\{2,4,7\},\{5\},\{6,8\},\{10\}\}[/tex]
é uma partição de [tex]X[/tex], com cinco elementos.
Uma bipartição é uma partição com exatamente dois elementos.
