 |
O que vai acontecer se dermos cinco bolinhas de gude para quatro meninos? |
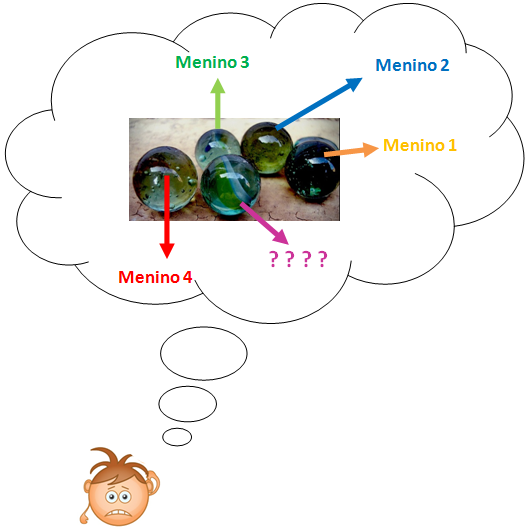
Xiiiii, vai dar confusão…
Mesmo que não se queira, um dos meninos receberá mais de uma bolinha!
Mas o que isso tem a ver com Matemática?
Princípio das Casas de Pombos
Leia com atenção as duas afirmações abaixo:
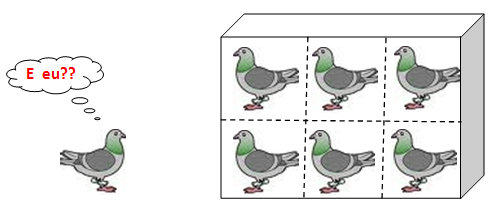
- Afirmação 1: Se temos que colocar sete pombos em seis casas, então alguma das casas terá que conter dois pombos ou mais.
- Afirmação 2: Se temos que colocar quatro livros em três gavetas, então alguma das gavetas terá que conter mais do que um livro.
Você duvidaria da veracidade dessas afirmações?
Se sim, veja:
Afirmação 1: Se tentarmos colocar apenas um pombo por casa, observe o que acontecerá com o sétimo pombo…
Afirmação 2: Vamos tentar colocar um livro em cada gaveta:
◆ o primeiro será colocado na primeira gaveta;
◆ o segundo livro será colocado na segunda gaveta;
◆ o terceiro livro será colocado na terceira gaveta;
◆ para o quarto livro não teremos gaveta vazia para colocá-lo.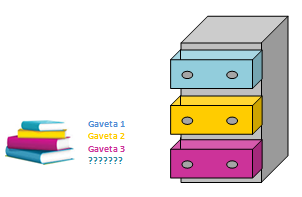
As afirmações 1 e 2 são situações particulares de uma ferramenta básica da Matemática: o Princípio das Casas de Pombos. Esse princípio foi utilizado pela primeira vez pelo matemático alemão Johann Peter Gustav Lejeune Dirichlet (1805-1859), em 1834, e por isso é também conhecido como Princípio das Gavetas de Dirichlet.
Esse Princípio trata de números inteiros positivos e seu enunciado é simples e intuitivo. Quem não conhece a sua aplicabilidade pode até acreditar que se trata de uma “pegadinha”.
Em sua versão mais simples o Princípio pode ser apresentado de uma das seguintes formas:
Princípio das Casas de Pombos: Se tivermos [tex]n+1 [/tex] pombos para serem colocados em [tex]n[/tex] casas, então pelo menos uma casa deverá conter dois ou mais pombos.
Princípio das Gavetas de Dirichlet: Se tivermos [tex]n+1[/tex] objetos para serem colocados em [tex]n [/tex] gavetas, então pelo menos uma gaveta deverá conter dois ou mais objetos.
Mesmo parecendo óbvio, vamos justificar o Princípio, usando a primeira forma, já que as duas são equivalentes.
Vamos então distribuir os [tex]n + 1 [/tex] pombos nas [tex]n [/tex] casas que temos à disposição.
Se colocarmos mais de um pombo em uma das casas, o Princípio já estará cumprido, então vamos, teimosamente, tentar colocar apenas um pombo em cada uma das [tex]n [/tex] casas.
Assim, executando a pior das hipóteses, se colocarmos exatamente um pombo em cada casa, sobrará um pombo que deverá ser colocado em qualquer uma das casas. Como todas já estão ocupadas, então uma das [tex]n [/tex] casas ficará com dois pombos.
Uma outra forma de justificarmos o Princípio das Casas de Pombos é raciocinarmos indiretamente: suponhamos que tivéssemos conseguido fazer a distribuição de todos os pombos nas [tex]n [/tex] casas, de modo a não existir mais de um pombo em cada casa. Então teríamos, no máximo, [tex]n [/tex] pombos, o que é uma contradição, uma vez que, por hipótese, tínhamos [tex]n+1[/tex] pombos.
|
Vejamos alguns exemplos simples de como aplicar o Princípio na resolução de problemas. |
A maneira com que justificamos o Princípio das Casas de Pombos nos dá uma estratégia para utilizá-lo na resolução de problemas; a partir dos dados do problema a ser resolvido, devemos:
- identificar quais são as “casas” e quais são os “pombos”,
- distribuir os pombos nas casas,
- determinar a relação existente entre ambos: pombos e casas.
Exemplo 1: Qual o número mínimo de pessoas que devemos reunir para que tenhamos certeza de que duas entre elas fazem aniversário no mesmo mês?
Resposta: O número mínimo de pessoas é 13.
Justificativa: Para este problema temos:
◆ casas: meses do ano (12);
◆ pombos: pessoas (13);
◆ relação: associamos cada pessoa ao seu mês de nascimento.
Pelo Princípio das Casas de Pombos, como temos 12 casas e 13 pombos, uma das casas receberá, pelo menos, 2 pombos, ou seja, um dos meses terá dois aniversariantes.
Exemplo 2: Uma caixa contém 3 tipos de bolas (azuis, verdes, amarelas). Qual o número mínimo de bolas que devemos retirar da caixa para garantirmos que temos duas bolas da mesma cor?
Solução: Devemos retirar 4 bolas.
Justificativa: Para este problema escolhemos:
◆ casas: uma caixa azul, uma caixa verde e uma caixa amarela (3);
◆ pombos: bolas (4);
◆ relação: associamos a cada bola a sua cor.
Pelo Princípio das Casas de Pombos, como temos 3 casas e 4 pombos, uma das casas receberá, pelo menos, 2 pombos, ou seja, uma das caixas conterá, pelo menos, duas bolas. Dessa forma, pelos menos duas bolas retiradas têm a mesma cor.
Vamos explicitar o raciocínio garantido pelo Princípio:
Ao retirarmos três bolas da caixa, a pior hipótese é que cada uma seja de uma cor.
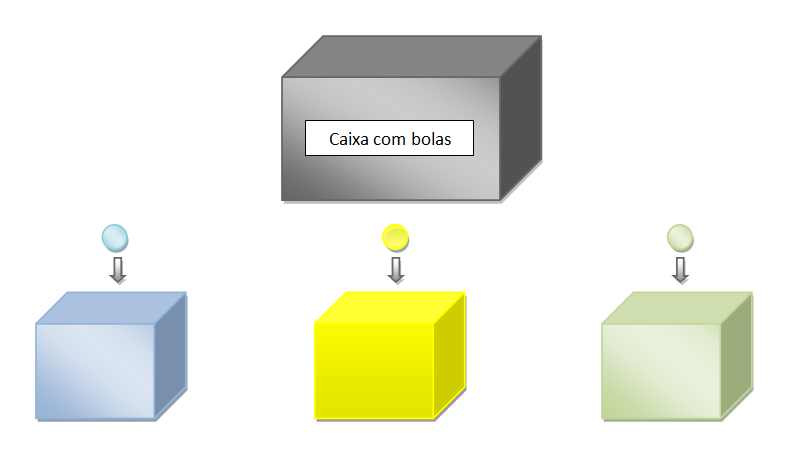Distribuindo, então, cada bola em sua respectiva caixa, com a retirada da quarta bola, esta poderá ser de qualquer cor.
Assim, precisamos retirar, no mínimo, 4 bolas para garantirmos que tenhamos duas bolas de mesma cor.
Exemplo 3: Em uma floresta existem 106 jaqueiras. É conhecido que cada uma dessas jaqueiras não produz anualmente mais do que 92 frutos. Prove que existem 2 jaqueiras na floresta que têm a mesma quantidade de frutos.
Solução:
Para este problema temos:
◆ casas: quantidade de frutos (0, 1, 2, 3, …, 92);
◆ pombos: jaqueiras (106);
◆ relação: associamos cada jaqueira à quantidade de frutos que ela contém.
Temos 106 jaqueiras e 93 casas identificadas pelos números 0; 1; 2; 3; … ; 92. O número k associado a cada casa significa que nela serão colocadas jaqueiras que têm exatamente k frutos.
Como [tex]106 > 94 = 93 + 1[/tex], o Princípio das Casas de Pombos nos garante que existem, pelo menos, duas jaqueiras com a mesma quantidade de frutos.
O assunto do próximo exemplo é, digamos, mais matemático.
Exemplo 4: São escolhidos cinco pontos, ao acaso, sobre a superfície de um quadrado de lado 2.
Mostre que pelo menos um dos segmentos determinados por dois desses pontos tem comprimento, no máximo, igual a [tex] \sqrt{2}[/tex].
Solução:
Inicialmente, vamos dividir o quadrado em quatro quadrados de lado 1:
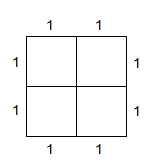
Com isso, façamos:
◆ casas: os quadrados menores (4);
◆ pombos: pontos (5);
◆ relação: associamos cada ponto ao quadrado a que ele pertence.
Pelo Princípio das Casas de Pombos, a superfície de um dos quadrados contém, pelo menos, dois dos cinco pontos dados.
Observe que, para cada quadrado, a distância máxima entre dois pontos sobre a sua superfície é igual ao comprimento de sua diagonal, que mede [tex] \sqrt{2}[/tex], veja:
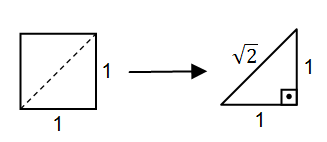
assim, os dois pontos que estão sobre a superfície de um mesmo quadrado estão a uma distância de no máximo [tex]\sqrt{2}[/tex].
Dessa forma, dados cinco pontos, como pelo menos dois estarão em uma mesma “casa”, eles determinam um segmento de comprimento, no máximo, igual a [tex] \sqrt{2}[/tex].
Equipe COM – OBMEP
Setembro de 2017.
|
Esperamos que você tire proveito da explanação feita aqui. |