✏ Link da Sala para dispositivos da Apple.
A soma [tex]1+2+3+ \cdots+t[/tex]
Para aqueles que sabem o que é uma Progressão Aritmética – PA , basta observar que a fórmula da soma dos [tex]n[/tex] primeiros termos da PA [tex](a_1, \, a_2, \, a_3, \, \ldots \, , \, a_n, \, \ldots)[/tex] é dada por
[tex]\qquad \qquad S_n=a_1+a_2+\ldots+a_n=\dfrac{(a_1+a_n)\cdot n}{2}[/tex].
Como [tex](1, \, 2, \, 3, \, 4, \, \ldots \, , \, t, \, t+1, \, \ldots)[/tex] é uma PA, de razão [tex]1[/tex], segue que a soma dos [tex]t[/tex] primeiros termos é dada por:
[tex]\qquad \qquad \boxed{1+2+3+ \cdots+t=\dfrac{(1+t)\cdot t}{2}}[/tex].
Assim, particularmente:
✓ [tex]1+2+3+ \cdots+10=\dfrac{(1+10)\cdot 10}{2}=\dfrac{11\cdot 10}{2}=11\cdot 5=55[/tex];
✓ [tex]1+2+3+ \cdots+100=\dfrac{(1+100)\cdot 100}{2}=\dfrac{101\cdot 100}{2}=101\cdot 50=5050[/tex];
✓ [tex]1+2+3+ \cdots+1000=\dfrac{(1+1000)\cdot 1000}{2}=\dfrac{1001\cdot 1000}{2}=1001\cdot 500=500500[/tex];
✓ [tex]1+2+3+ \cdots+5000=\dfrac{(1+5000)\cdot 5000}{2}=\dfrac{5001\cdot 5000}{2}=5001\cdot 2500=12502500[/tex].
Que fórmula fantástica, não é?
Com ela obtemos com a mesma facilidade uma soma com dez, com mil ou com cinco mil parcelas!
Mas, embora útil, alguém que não saiba o que é uma PA poderá ficar na dúvida se essa fórmula funciona sempre. Assim, vamos mostrar como obtê-la por dois caminhos diferentes e sem utilizar progressões aritméticas. Em cada caminho, vamos simplesmente fazer continhas agrupando de forma conveniente as parcelas da soma [tex]1+2+3+ \cdots+t[/tex].
Vejamos.
Método I
Se [tex]t[/tex] é um número natural maior do que [tex]1[/tex], observe inicialmente que
[tex]\qquad \qquad 1+2+\cdots+(t-1)+t=t+(t-1)+\cdots+2+1[/tex],
portanto:
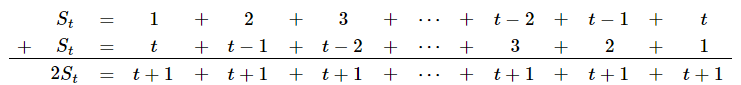
Assim, [tex]2S_t=t\cdot (t+1)[/tex] e podemos concluir que:
[tex]\qquad \qquad \boxed{S_t=\dfrac{t\cdot (t+1)}{2}}[/tex].
Para você entender direitinho o que aconteceu com as parcelas centrais de [tex] S_t[/tex], quando somamos as duas igualdades, vamos refazer a soma considerando dois casos: [tex]t[/tex] par e [tex]t[/tex] ímpar.
✓ Para [tex]t[/tex] par, observe que:
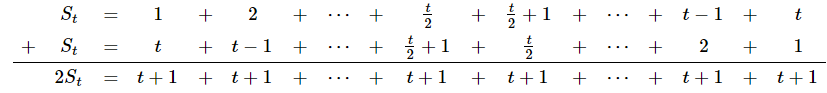
Com isso, [tex]2S_t=t\cdot(t+1)[/tex] e podemos assim concluir que [tex]S_t=\dfrac{t\cdot(t+1)}{2}[/tex].
✓ Para [tex]t[/tex] ímpar, observe que:
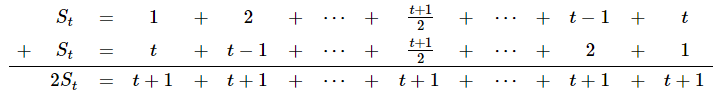
Aqui também, [tex]2S_t=t\cdot(t+1)[/tex] e [tex] S_t=\dfrac{t\cdot(t+1)}{2}[/tex].
Método II
Seja [tex]t[/tex] um número natural maior do que [tex]1.[/tex]
✓ Suponha que [tex]t[/tex] seja par; assim podemos agrupar os [tex]t[/tex] números [tex]1, \, 2, \, 3, \, 4, \, \ldots \, , \, t[/tex] de dois em dois, conforme mostra a figura abaixo, e somá-los.

[tex] \quad\begin{align*} &1+2+3 \cdots+t= {\color{red}{1}}+{\color{#1E90FF}{2}}+{\color{#FF8C00}{3}}+{\color{#32CD32}{4}}+ \cdots+{\color{#32CD32}{(t-3)}}+{\color{#FF8C00}{(t-2)}}+{\color{#1E90FF}{(t-1)}}+{\color{red}{t}}=\\
&=\underbrace{{\color{red}{[1+t]}}+{\color{#1E90FF}{[2+(t-1)]}}+{\color{#FF8C00}{[3+(t-2)]}}+{\color{#32CD32}{[4+(t-3)]}}+ \cdots+\left[\dfrac{t}{2}+\left(\dfrac{t}{2}+1\right)\right]}_{\frac{t}{2} \, parcelas}\\
&=\underbrace{[1+t]+[1+t]+[1+t]+[1+t]+ \cdots+[1+t]}_{\frac{t}{2} \, parcelas}\\
&=\dfrac{t}{2}\cdot (1+t)\\
&=\dfrac{(1+t)\cdot t}{2}. \end{align*}[/tex]
✓ Se [tex]t[/tex] for ímpar, podemos agrupar os [tex]t[/tex] números [tex]1, \, 2, \, 3, \, 4, \, \ldots \, , \, t[/tex] conforme mostra a figura abaixo, e somá-los.

[tex] \quad\begin{align*} &1+2+3 \cdots+t= {\color{red}{1}}+{\color{#1E90FF}{2}}+{\color{#FF8C00}{3}}+ \cdots+{\color{#FF8C00}{(t-2)}}+{\color{#1E90FF}{(t-1)}}+{\color{red}{t}}=\\
&=\underbrace{{\color{red}{[1+t]}}+{\color{#1E90FF}{[2+(t-1)]}}+{\color{#FF8C00}{[3+(t-2)]}}+ \cdots+{\color{#32CD32}{\left[\dfrac{t-1}{2}+\dfrac{t+3}{2}\right]}}}_{\frac{t-1}{2} \, parcelas}+\dfrac{t+1}{2}\\
&=\underbrace{[1+t]+[1+t]+[1+t]+[1+t]+ \cdots+[1+t]}_{\frac{t-1}{2} \, parcelas}+\dfrac{t+1}{2}\\
&=\dfrac{t-1}{2}\cdot (1+t)+\dfrac{1+t}{2}\\
&=\dfrac{(1+t)\cdot t}{2}. \end{align*}[/tex]
✓ Se [tex]t[/tex] for ímpar, podemos também agrupar de dois em dois, bastando para isso observar que
[tex]\qquad \qquad 1+2+3+4+\cdots +t=0+1+2+3+4+\cdots +t.[/tex]
Perceba que, dessa forma, conseguimos obter a mesma soma com quantidades diferentes de parcelas: do lado esquerdo da igualdade temos [tex]t[/tex] parcelas, ou seja, uma quantidade ímpar de parcelas; mas, do lado direito, temos [tex]t+1[/tex] parcelas, logo, uma quantidade par de parcelas.
Basta então agruparmos as parcelas da soma [tex]0+1+2+3+4+\cdots+t.[/tex]

[tex] \quad\begin{align*}&1+2+3 \cdots+t= 0+1+2+3 \cdots+t=\\
&={\color{red}{0}}+{\color{#1E90FF}{1}}+{\color{#FF8C00}{2}}+{\color{#32CD32}{3}}+ \cdots+{\color{#32CD32}{(t-3)}}+{\color{#FF8C00}{(t-2)}}+{\color{#1E90FF}{(t-1)}}+{\color{red}{t}}\\
&=\underbrace{{\color{red}{[0+t]}}+{\color{#1E90FF}{[1+(t-1)]}}+{\color{#FF8C00}{[2+(t-2)]}}+{\color{#32CD32}{[3+(t-3)]}}+ \cdots+\left[\dfrac{t-1}{2}+\dfrac{t+1}{2}\right]}_{\frac{t+1}{2} \, parcelas}\\
&=\underbrace{[t]+[t]+[t]+[t]+ \cdots+[t]}_{\frac{t+1}{2} \, parcelas}\\
&=\dfrac{t+1}{2}\cdot t\\
&=\dfrac{(1+t)\cdot t}{2}. \end{align*}[/tex]
Ufa, quantas contas, hem?
E depois de tantos cálculos, que tal uma historinha para descontrair ? ! ? !

Extraído da Revista Galileu
O cálculo feito pelo menino Gauss foi:
[tex] \boxed{1+2+3+\cdots +99+100=\dfrac{100}{2} \times 101 = 50\times 101=5050.}[/tex]
Podemos observar que a peripécia do pequeno Gauss é o caso particular de [tex]t=100[/tex] da nossa primeira lousinha, conforme ilustra o esqueminha abaixo.
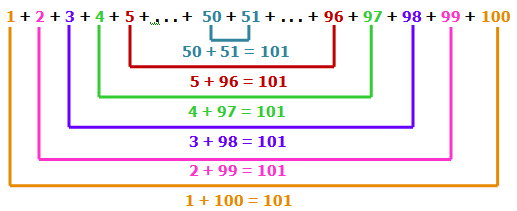
Para a história não ficar sem fim, o menino autor da façanha se tornou um dos mais importantes matemáticos de todos os tempos: Johann Carl Friedrich Gauss, conhecido como o Príncipe da Matemática!
Bem, dizem que uma boa conversa sobre Matemática não pode terminar sem bons problemas. Assim, clique no próximo botão e divirta-se!
Equipe COM – OBMEP
Agosto de 2018.
