Definição: Chamamos de progressão geométrica (P.G.) toda sequência em que cada termo, a partir do segundo, é igual ao produto do termo anterior por uma constante real. Tal constante é chamada razão da P.G. e é usualmente indicada por [tex]q[/tex].
Observação: Progressões geométricas também podem ser finitas ou infinitas.
Exemplos:
● Se [tex]a_1=2[/tex] e [tex]q=\dfrac{1}{2},[/tex] temos a P.G. [tex]\left(2,1,\dfrac{1}{2},\dfrac{1}{4},\dfrac{1}{8},\cdots\right).[/tex]
● Se [tex]a_1=-\dfrac{1}{3}[/tex] e [tex]q=1,[/tex] temos a P.G. [tex]\left(-\dfrac{1}{3},-\dfrac{1}{3},-\dfrac{1}{3},\cdots\right).[/tex]
● Se [tex]a_1=-1[/tex] e [tex]q=-2,[/tex] temos a P.G. [tex](-1, 2, -4, 8, -16,\cdots).[/tex]
Classificação
As progressões geométricas, assim como as aritméticas, podem ser classificadas em categorias, conforme veremos a seguir.
● quando todos os termos são iguais a [tex]0[/tex] (neste caso, o primeiro termo é [tex]a_1=0[/tex] e a razão é [tex]q[/tex] qualquer);
● quando os termos são diferentes de [tex]0[/tex] (neste outro caso, o primeiro termo é [tex]a_1\neq 0[/tex] e a razão é [tex]q=1[/tex]).
Exemplos:
[tex]\qquad (0,0,0,\cdots )[/tex] é uma progressão geométrica constante, na qual [tex]a_1 = 0[/tex] e [tex]q = 2[/tex] (ou qualquer outro número real);
[tex]\qquad \left(\dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{2},\cdots\right)[/tex] é uma progressão geométrica constante, na qual [tex]a_1=\dfrac{1}{2}[/tex] e [tex]q=1.[/tex]
➤ Crescentes: são progressões geométricas em que cada termo, a partir do segundo, é maior que o termo anterior, podendo ocorrer em duas situações:
● quando o primeiro termo é [tex]a_1\gt 0[/tex] e a razão é [tex]q\gt 1;[/tex]
● quando o primeiro termo é [tex]a_1\lt 0[/tex] e a razão é [tex]0\lt q\lt 1.[/tex]
Exemplos:
[tex]\qquad (8,12,18,27,\cdots)[/tex] é uma progressão geométrica crescente, na qual [tex]a_1=8[/tex] e [tex]q=\dfrac{3}{2};[/tex]
[tex]\qquad \left(-1, -\dfrac{1}{2}, -\dfrac{1}{4}, -\dfrac{1}{8}, \cdots\right)[/tex] é uma progressão geométrica crescente, na qual [tex]a_1 = -1[/tex] e [tex]q = \dfrac{1}{2}.[/tex]
➤ Decrescentes: são progressões geométricas em que cada termo, a partir do segundo, é menor que o termo anterior, e isso ocorre:
● quando o primeiro termo é [tex]a_1\gt 0~[/tex] e [tex]~0\lt q\lt1;[/tex]
● quando o primeiro termo é [tex]a_1\lt 0[/tex] e a razão é [tex]q\gt 1.[/tex]
Exemplos:
[tex]\qquad \left(1, \dfrac{1}{3}, \dfrac{1}{9}, \dfrac{1}{27}, \cdots\right)[/tex] é uma progressão geométrica decrescente, na qual [tex]a_1 = 1[/tex] e [tex]q = \dfrac{1}{3};[/tex]
[tex]\qquad(-1, -3, -9, -27, \cdots)[/tex] é uma progressão geométrica decrescente, na qual [tex]a_1 = -1[/tex] e [tex]q = 3.[/tex]
➤ Oscilantes ou Alternadas: são progressões geométricas em que cada termo, a partir do segundo, possui sinal diferente do anterior, ocorrendo tal situação quando [tex]a_1\neq 0[/tex] e [tex]q\lt 0.[/tex]
Exemplos:
[tex]\qquad (2, -2, 2, -2, 2, \cdots)[/tex] é uma progressão geométrica oscilante, na qual [tex]a_1 = 2[/tex] e [tex]q = -1.[/tex]
[tex]\qquad (-1, 2, -4, 8, -16, \cdots)[/tex] é uma progressão geométrica oscilante, na qual [tex]a_1 = -1[/tex] e [tex]q = -2.[/tex]
➤ Estacionárias: são progressões geométricas em que o primeiro termo é diferente de zero e todos os termos a partir do segundo são iguais a zero, e isso ocorre quando [tex]a_1\neq 0[/tex] e [tex]q=0.[/tex]
Exemplos:
[tex]\qquad (3, 0, 0, 0, \cdots)[/tex] é uma progressão geométrica estacionária, na qual [tex]a_1 = 3[/tex] e [tex]q = 0.[/tex]
[tex]\qquad (-2, 0, 0, 0, \cdots)[/tex] é uma progressão geométrica estacionária, na qual [tex]a_1 = -2[/tex] e [tex]q = 0.[/tex]
Termo geral de uma P.G.
Pela definição, podemos notar que em uma progressão geométrica [tex](a_i )[/tex], mesmo infinita, qualquer termo pode ser imediatamente determinado, a partir do primeiro termo:
[tex]\qquad \begin{align} a_2&= a_1\cdot q\,;\\
a_3&= a_2\cdot q = (a_1\cdot q)\cdot q = a_1\cdot q^2;\\
a_4&=a_3\cdot q=(a_1\cdot q^2 )\cdot q=a_1\cdot q^3;\\
&~~\vdots\\
a_n&=a_{n-1}\cdot q=(a_1\cdot q^{n-2} )\cdot q=a_1\cdot q^{n-1};\\
&~~\vdots
\end{align} [/tex]
De acordo com os cálculos, existe uma fórmula para encontrar o n-ésimo termo de qualquer P.G.; vamos registrar essa fórmula como uma propriedade.
[tex]\qquad \boxed{a_n=a_1\cdot q^{n-1}}[/tex]
sendo [tex]n \in \mathbb{N}^*.[/tex]
Apesar de sua utilidade, aqui também observamos na fórmula acima a inconveniência de necessitarmos do primeiro termo da progressão para utilizá-la. Veremos a seguir outra maneira de obtermos termos de uma progressão geométrica a partir de qualquer termo anterior da progressão. Vamos fazer a dedução utilizando a fórmula acima como o primeiro passo e considerando, a princípio, [tex]q\ne 0[/tex]:
[tex]\qquad a_n = a_1\cdot q^{n-1}\\
\qquad a_n = a_1\cdot q^{n-1}\cdot \dfrac{q^p}{q^p}\\
\qquad a_n = \underbrace{a_1\cdot q^{p-1}}_{a_p} \cdot \dfrac{q^n}{q^p}\\
\qquad a_n=a_p\cdot \dfrac{q^n}{q^p}\\
\qquad a_n=a_p\cdot q^{n-p}.[/tex]
Observe que na dedução impusemos [tex]q\ne 0[/tex] para não zerarmos o denominador em algumas passagens. Mas, no caso de [tex]q=0[/tex], teríamos uma sequência na qual todos os termos seriam zero e a fórmula final seria válida.
Vamos registrar, também, a fórmula obtida como uma propriedade.
[tex]\boxed{a_n=a_p\cdot q^{n-p}}[/tex]
para [tex]n,~p \in \mathbb{N}^*[/tex] tais que [tex] p \lt n.[/tex]
Soma dos [tex]n[/tex] primeiros termos de uma P.G.
Dada a P.G. [tex]\left(a_i \right)[/tex] cuja razão é [tex]q[/tex], com [tex]q\neq 1[/tex], vamos tentar obter a soma dos seus [tex]n[/tex] termos iniciais.
[tex]\quad S_n = a_1+a_2+a_3+\cdots +a_{n-1}+a_n. ~~~~\textcolor{#589386}{(i)}[/tex]
Note que, multiplicando essa igualdade por [tex]q[/tex], segue que:
[tex]\quad q\cdot S_n = q\cdot (a_1+a_2+a_3+\cdots +a_{n-1}+a_n)\\
\quad q\cdot S_n = q\cdot a_1+q\cdot a_2+q\cdot a_3+\cdots +q\cdot a_{n-1}+q\cdot a_n\\
\quad q\cdot S_n =a_2+a_3+\cdots +a_{n-1}+a_n+q\cdot a_n.~~~~\textcolor{#589386}{(ii)}[/tex]
Fazendo a diferença entre as expressões [tex]{(ii)}~[/tex] e [tex]~{(i)}[/tex] obtemos:
[tex]\quad q\cdot S_n-S_n = (\cancel{a_2}+\cancel{a_3}+\cdots +\cancel{a_{n-1}}+\cancel{a_n}+q\cdot a_n)-(a_1+\cancel{a_2}+\cancel{a_3}+\cdots +\cancel{a_{n-1}}+\cancel{a_n})\\
\quad (q-1)\cdot S_n=q\cdot a_n-a_1\\
\quad S_n=\dfrac{q\cdot a_n-a_1}{q-1}.[/tex]
Substituindo a fórmula do termo geral de uma P.G. na expressão acima, segue que:
[tex]\quad S_n=\dfrac{q\cdot (a_1\cdot q^{n-1})-a_1}{q-1}\\
\quad S_n=\dfrac{a_1\cdot q^n-a_1}{q-1}\\
\quad S_n=\dfrac{a_1\cdot (q^n-1)}{q-1}.[/tex]
É importante observamos que, quando [tex]q=1[/tex], a fórmula não pode ser deduzida, uma vez que teríamos [tex]q-1=0[/tex] e então zeraríamos o denominador. Mas, neste caso particular, ou seja, quando [tex]q=1[/tex], temos todos os termos da P.G. iguais a [tex]a_1[/tex] e então a soma dos [tex]n[/tex] primeiros termos seria [tex]S_n = n\cdot a_1.[/tex]
Temos, então, mais uma propriedade:
Denotando por [tex]S_n[/tex] a soma dos [tex]n[/tex] primeiros termos dessa P.G., temos
[tex]\qquad \boxed{S_n=\dfrac{a_1\cdot (q^n-1)}{q-1}}. [/tex]
Exemplo: Observe que na P.G. [tex]\left(2,6,18,54,\cdots \right)[/tex] temos [tex]a_1= 2[/tex] e [tex]q=3.[/tex]
Assim, a soma [tex]S_8[/tex] dos oito primeiros termos desta sequência é
[tex]\qquad S_8=\dfrac{2\cdot (3^8-1)}{3-1}\\
\qquad \boxed{S_8=6560}.[/tex]
Produto dos [tex]n[/tex] primeiros termos de uma P.G.
[tex]\boxed{P_n=a_1^n\cdot q^{\frac{n(n-1)}{2}}}.[/tex]
Vamos verificar a validade dessa fórmula. Repare que:
[tex]~~\\
\quad P_n = a_1\cdot a_2\cdot a_3\cdot \cdots\cdot a_n\\
\quad P_n = a_1\cdot a_1\cdot q\cdot a_1\cdot q^2\cdot \cdots\cdot a_1\cdot q^{n-1}\\
\quad P_n = a_1^n\cdot q\cdot q^2\cdot \cdots\cdot q^{n-1}\\
\quad P_n = a_1^n\cdot q^{1+2+\cdots+(n-1)}\\
\quad P_n = a_1^n\cdot q^{\frac{n(n-1)}{2}}.[/tex]
Exemplo: Observe que, na P.G. [tex](-1,2,-4,\cdots)[/tex], temos [tex]a_1= -1[/tex] e [tex]q=-2.[/tex] Assim, o produto [tex]P_5[/tex] dos cinco primeiros termos desta sequência é dado por:
[tex]\quad P_5 = (-1)^5\cdot (-2)^{\frac{5\cdot 4}{2}}[/tex]
[tex]\quad P_5 = -1\cdot (-2)^{10}[/tex]
[tex]\quad P_5 = -1\cdot 1024[/tex]
[tex]\quad \boxed{P_5=-1024}.[/tex]
Somas infinitas
Na Sala 1, provamos a validade de uma fórmula utilizada para determinar a soma dos [tex]n[/tex] primeiros termos de uma P.A.. Não existe uma fórmula que determine a soma de todos os termos de uma P.A. infinita, uma que vez que essa soma pode ser ilimitada!
Porém, agora que já temos a fórmula da soma dos [tex]n[/tex] primeiros termos de uma P.G., podemos deduzir a fórmula da soma de todos os termos de certas progressões geométrica infinitas. Você deve estar se perguntando:
Como é que eu vou somar infinitos termos?????
Vamos começar essa discussão com um exemplo: a P.G. [tex]\left(\dfrac{1}{2},~\dfrac{1}{4},~\dfrac{1}{8}, ~\dfrac{1}{16},~\cdots~\right).[/tex]
Essa sequência infinita é, de fato, uma P.G. cujo primeiro termo é [tex]\dfrac{1}{2}[/tex] e a razão é [tex]\dfrac{1}{2}.[/tex] Vamos tentar determinar a soma de todos os seus termos, ou seja a soma [tex]\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots~.[/tex] Observe que, embora tenhamos que somar infinitas parcelas, essas parcelas vão ficando cada vez menores; dessa forma, estamos “acrescentando, a cada soma finita, números muito pequenos e cada vez menores”…
Vamos observar geometricamente essa soma:
- Na figura abaixo, vemos um quadrado unitário que foi dividido em dois retângulos de área [tex]\dfrac{1}{2}.[/tex]
- Colorimos um retângulo de amarelo e o outro foi dividido em dois quadrados de área [tex]\dfrac{1}{4}.[/tex]
- Colorimos um quadrado de azul e o outro foi dividido em dois retângulos de área [tex]\dfrac{1}{8}.[/tex]
- Colorimos um retângulo de verde e o outro foi dividido em dois quadrados de área [tex]\dfrac{1}{16}.[/tex]
- Colorimos um quadrado de rosa e o outro foi dividido em dois retângulos de área [tex]\dfrac{1}{32}.[/tex]
- Colorimos um retângulo de lilás e o outro foi dividido em dois quadrados de área [tex]\dfrac{1}{64}.[/tex]
- Colorimos um quadrado de marrom claro e o outro foi dividido em dois retângulos de área [tex]\dfrac{1}{128}.[/tex]
- Colorimos um retângulo de alaranjado e o outro foi dividido em dois quadrados de área [tex]\dfrac{1}{256}.[/tex]
- Colorimos um quadrado de cinza claro e o outro foi dividido em dois retângulos de área [tex]\dfrac{1}{512}.[/tex]
- Colorimos um retângulo de azul escuro e o outro foi dividido em dois quadrados de área [tex]\dfrac{1}{1024}.[/tex]
- Colorimos um quadrado de ciano e o outro foi dividido em dois retângulos de área [tex]\dfrac{1}{2048}.[/tex]
- Colorimos um retângulo de magenta e o outro vai ser dividido em dois quadrados de área [tex]\dfrac{1}{4096}[/tex], e assim sucessivamente.
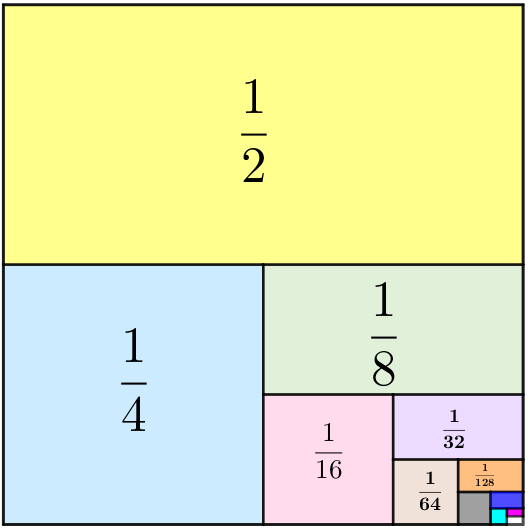
Dessa forma, podemos concluir que a soma [tex]\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots~[/tex] será a soma das áreas de todos os retângulos e quadrados que construímos e de todos os infinitos retângulos e quadrados que sequer conseguiremos construir…
Assim, [tex]\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots~[/tex] é a medida da área do quadrado unitário, ou seja: [tex]\boxed{\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16_~}+\cdots~=1}.[/tex]
Voltemos ao caso geral!
Observe que se [tex]-1\lt q\lt 1[/tex], então [tex]|q|\lt 1[/tex]; e, supondo [tex]q\neq 0[/tex], é notório que
[tex]\qquad \qquad |q|\gt |q|^2\gt |q|^3\gt |q|^4\gt |q|^5\gt \cdots [/tex].
Dessa forma, à medida que aumentamos o valor de [tex]n[/tex], [tex]|q|^n[/tex] fica cada vez mais próximo de [tex]0[/tex]. Em uma linguagem um pouco mais rebuscada, podemos dizer que quando [tex]n[/tex] tende ao infinito, [tex]|q|^n[/tex] tende a [tex]0.[/tex]
Assim, a partir da fórmula da soma dos primeiros termos de uma P.G., podemos intuir que a soma [tex]S[/tex] de todos os termos de uma P.G. infinita, com [tex]-1\lt q\lt 1[/tex] pode ser assim obtida:
[tex]\qquad S=\dfrac{a_1\cdot (0-1)}{q-1}\\
\qquad S=-\dfrac{a_1}{q-1}\\
\qquad S=\dfrac{a_1}{1-q}[/tex]
e apresentar o próximo resultado.
[tex]\boxed{S=\dfrac{a_1}{1-q}}.[/tex]
É importante observarmos que a Matemática fornece ferramentas adequadas para o estudo formal dessa discussão informal que apresentamos. No entanto, o estudo dessas ferramentas apresenta um nível de abstração e um nível de conhecimento que fogem aos objetivos desta nossa discussão!
Exemplos:
(1) Observe que na P.G. [tex]\left(1,\dfrac{1}{2},\dfrac{1}{4},\dfrac{1}{8},\cdots\right),[/tex] temos [tex]a_1= 1[/tex] e [tex]q=\dfrac{1}{2}.[/tex] Assim, a soma [tex]S[/tex] dos termos desta sequência infinita, é
[tex]\qquad S=\dfrac{1}{1-\dfrac{1}{2}} = \dfrac{1}{\dfrac{1}{2}} = 2.[/tex]
(2) Determine a fração geratriz da dízima periódica [tex] 0,7777~\cdots~.[/tex]
Observe que :
[tex] \qquad 0,7777~\cdots~=0,7+0,07+0,007+0,0007+~\cdots\\
\qquad 0,7777~\cdots~=\dfrac{7}{10}+\dfrac{7}{100}+\dfrac{7}{1000}+\dfrac{7}{10000}+~\cdots [/tex]
e, particularmente, a sequência [tex] \left(\dfrac{7}{10},~\dfrac{7}{100},~\dfrac{7}{1000},~\dfrac{7}{10000}, ~\cdots \right) [/tex] é uma P.G. cujo primeiro termo é [tex]\dfrac{7}{10}[/tex], a razão é [tex]q=\dfrac{1}{10}[/tex], sendo [tex]-1 \lt q=\dfrac{1}{10} \lt 1.[/tex]
Com isso, de [tex] 0,7777~\cdots~=\dfrac{7}{10}+\dfrac{7}{100}+\dfrac{7}{1000}+\dfrac{7}{10000}+~\cdots ,[/tex] segue que:
[tex]\qquad 0,7777~\cdots~=\dfrac{a_1}{1-q}=\frac{\frac{7}{10}}{1-\frac{1}{10}}\\
\qquad 0,7777~\cdots~=\dfrac{\frac{7}{10}}{\frac{9}{10}}\\
\qquad \boxed{0,7777~\cdots~=\dfrac{7}{9}}. [/tex]
Portanto, a fração geratriz da dízima periódica [tex] 0,7777~\cdots~[/tex] é [tex]~\dfrac{7}{9}.[/tex]
Finalizamos a Sala 1 apresentando uma relação entre cada termo de uma P.A., a partir do segundo, e seus dois vizinhos imediatos. Vamos finalizar esta Sala apresentando também uma relação entre cada termo de uma P.G., a partir do segundo, e seus dois vizinhos imediatos:
[tex]\qquad \boxed{a_n = \sqrt {a_{n-1}\cdot a_{n+1}}}.[/tex]
para [tex]n \in \mathbb{N},~ n \gt 1.[/tex]
Também podemos garantir essa propriedade de maneira bem simples. De fato:
[tex]\qquad \qquad \begin{align}\boxed{\sqrt{a_{n-1}\cdot a_{n+1}}} &= \sqrt{a_{n-1}\cdot (a_{n-1}\cdot q^2)}\\
&=\sqrt{(a_{n-1})^2\cdot q^2}\\
& = |a_{n-1}|\cdot |q|\\
& = a_{n-1}\cdot q\\
& =\boxed{a_n}. \end{align} [/tex]
Observe que, como todos os termos são positivos, necessariamente [tex]q\gt 0[/tex] e, portanto, [tex]|q|=q.[/tex]
Equipe COM – OBMEP
