.Sala de Estudo: Logaritmos X Terremotos

Sabe qual é a pergunta que não quer calar?

Uma das perguntas que os alunos mais fazem em sala de aula é:
    – Professor, onde vou aplicar isso na minha vida?
Não é verdade?
Essa pergunta sempre surge quando os alunos estão estudando um determinado assunto e não possuem o esclarecimento de onde aquele assunto é aplicável.
Pois bem, na sala em que estamos, abordaremos algumas aplicações de um importante assunto da Matemática: os Logaritmos.

Mas, afinal, para que servem os Logaritmos?

Logaritmos possuem várias aplicações na Matemática e em diversas áreas do conhecimento, como Física, Biologia, Química, Medicina, Geografia, entre outras. Vamos ver algumas situações?

➤ Matemática Financeira
Uma pessoa aplicou a importância de R$ 500,00 em uma instituição bancária, que paga juros mensais de 0,7%, no regime de juros compostos. Quanto tempo após a aplicação o montante será de R$ 3.500,00?

➤ Geografia
Em uma determinada cidade, a taxa de crescimento populacional é de 3% ao ano, aproximadamente. Em quantos anos a população dessa cidade dobrará, se a taxa de crescimento continuar a mesma?

➤ Química
Determine o tempo em que 1.000 g de certa substância radioativa, que se desintegra à taxa de 2% ao ano, reduz-se a 200 g. Para isso, utilize a seguinte expressão:
[tex]\quad \qquad Q=Q_0 \cdot e^{–rt}[/tex],
na qual [tex]Q[/tex] é a massa da substância, [tex]r[/tex] é a taxa e [tex]t[/tex] é o tempo em anos.

Todos os três exemplos citados são resolvidos com o auxílio dos logaritmos.

Os logaritmos são usados especialmente para criar escalas de medição. Alguns exemplos de aplicações de logaritmos incluem a escala Richter para medir a magnitude de terremotos, a escala de decibéis para medir a intensidade de sons, ordens de magnitude e aplicações em análise de dados.
Particularmente nesta Sala, vamos explorar a aplicação no estudo dos terremotos.

Imagem extraída do site Veja. (Acesso em 02/02/2024.)

Histórico de grandes terremotos

Na reportagem atualizada em 09/09/2023 que aparece nesta página, estão apontados os cinco maiores terremotos que já ocorreram no mundo; a saber:

1º) Chile
Na noite de 22 de maio de 1960, o Chile foi atingido em cheio pelo maior terremoto já registrado no planeta: magnitude 9,5.
Aproximadamente 1,6 mil pessoas morreram, 3 mil ficaram feridas e mais de 2 milhões perderam suas casas. O prejuízo estimado para o Chile foi de US$ 550 milhões.
O terremoto foi seguido por um tsunami, que deixou 61 mortos no Estado americano do Havaí, 138 no Japão e 32 nas Filipinas.

2º) Alasca (EUA)
Com magnitude de 9,2, em 28 de março de 1964 um terremoto, que foi seguido por tsunami, tirou a vida de 131 pessoas e causou prejuízos da ordem de US$ 2,3 bilhões. Os efeitos do tremor foram fortemente sentidos em várias cidades americanas.

3º) Sumatra (Indonésia)
Em 26 de dezembro de 2004, um terremoto com magnitude de 9,1 atingiu a costa oeste da ilha de Sumatra, na Indonésia. O tsunami que se seguiu ao terremoto atingiu 14 países do Sul da Ásia e do leste da África. Ao todo, a tragédia deixou cerca de 230 mil mortos ou desaparecidos e 1,7 milhão desabrigados.

4º) Honshu (Japão)
Com magnitude de 9,0, em 11 de março de 2011, pelo menos 15,7 mil pessoas foram mortas, 4,6 mil dadas como desaparecidas e 5,3 mil feridas quando um terremoto seguido por tsunami arrasou a costa leste de Honshu, a maior e mais populosa ilha do Japão.
A combinação de tremor e maremoto também deixou mais de 130 mil pessoas desabrigadas e destruiu 300 mil casas e prédios. A maioria das mortes ocorreu nas cidades de Iwate, Miyagi e Fukushima.
As ondas chegaram a 38 metros de altura. O prejuízo total para o Japão foi estimado em US$ 309 bilhões.

5º) Kamchatka (Rússia)
Com magnitude de 9,0, em 4 de novembro de 1952, um terremoto seguido por um tsunami atingiu a península de Kamchatka, no extremo leste da Rússia. Não houve registro de mortes, em grande parte pelo fato de a região ser pouco povoada.
No entanto, o maremoto atingiu o Havaí, nos Estados Unidos, provocando perdas da ordem de US$ 1 milhão. As ondas destruíram barcos, casas, píeres e estradas.

Mas, o que são os terremotos?

Os terremotos são fenômenos naturais causados por falhas geológicas, vulcanismos, mas, principalmente, por movimentos de desgaste e acomodação das placas tectônicas – imensos blocos de rocha que estão em constante movimento de deslizamento.
A figura abaixo mostra o que seriam grandes “rachaduras” no planeta. Tais rachaduras são decorrentes do movimento das placas tectônicas que flutuam sobre o magma (rochas em estado líquido, com uma consistência meio pastosa). Quando elas se chocam liberam grande quantidade de energia resultando nos abalos sísmicos.

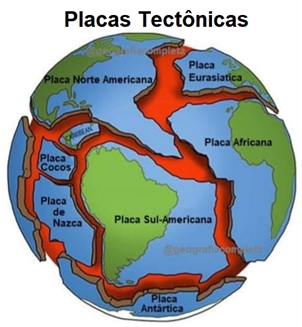
Imagem extraída do site Facebook. (Acesso em 02/02/2024.)

A litosfera terrestre (camada sólida mais externa da Terra) está dividida em 15 placas tectônicas principais e várias secundárias. As principais são as placas mostradas na imagem a seguir: Africana, Antártida, Arábica, Australiana, Caribenha, Cocos, Euroasiática, Filipinas, Nazca, Norte-Americana, do Pacífico, Indiana, Scotia, Juan de Fuca e Sul-Americana.

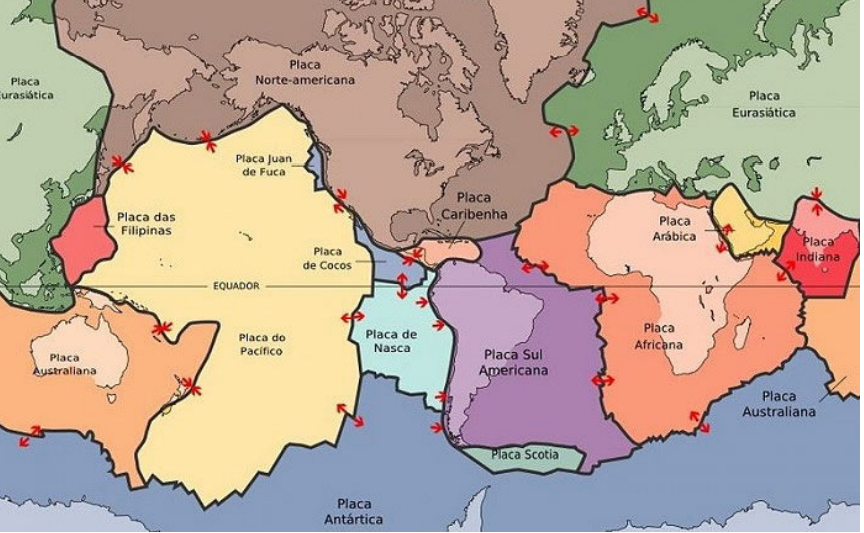
Imagem extraída do site do Sistema Maxwell, PUC-Rio. (Acesso em 02/02/2024.)

As regiões que se encontram nas bordas dessas placas são as que mais sofrem os efeitos desses abalos sísmicos; mas, embora quase a totalidade das atividades sísmicas do planeta ocorram em limites de placas tectônicas (terremotos interplacas), também pode haver terremotos no interior de uma placa (terremotos intraplaca). Estes são caracterizados como de “falhamento superficial” e, em geral, são de pequena magnitude e causam prejuízos menores, quando comparados com os que ocorrem nas bordas de placas.
Particularmente, como o Brasil está na Placa Sul-Americana e esta se choca com outra placa na região da Cordilheira dos Andes, fora do nosso território, estamos livres de terremotos muito fortes.
De toda forma, os terremotos são fenômenos naturais que ocorrem de forma até que rotineira; o que muda é com que força esses fenômenos ocorrem.

Como medir terremotos

Há duas formas de medir a força dos tremores: pela sua magnitude e pela sua intensidade. “A magnitude está associada com a energia liberada pelo terremoto”, enquanto “a intensidade é o efeito causado por ele na superfície da Terra”.

➤ A intensidade sísmica se baseia nos efeitos ou danos produzidos nas estruturas e percebidos pelas pessoas nas imediações do abalo. É uma classificação qualitativa e não deve ser interpretada em termos absolutos, uma vez que depende de observação e impressão humanas.
A escala de intensidade mais utilizada é a de Mercalli Modificada (MMI) e é identificada por algarismos romanos de I a XII:
   I. Tremor não percebido.
   II. Sentido por pessoas em repouso ou em andares superiores de edifícios.
   III. Vibração leve. Objetos pendurados balançam levemente.
   IV. Vibração como a causada pela passagem de caminhões pesados. Carros parados balançam.
   V. Pessoas acordam, pequenos objetos tombam e quadros nas paredes se movem.
   VI. Sentido por todos. Deslocamento de móveis. Louças e vidros se quebram. Queda de objetos. Rachadura no reboco de casas.
   VII. Percebido por motoristas dirigindo. Dificuldade em manter-se em pé. Sinos tocam em igrejas, capelas, etc. Quebra de chaminés e ornamentos arquitetônicos, queda de reboco, rachaduras em paredes.
   VIII. Galhos e troncos se quebram. Rachaduras em solo molhado. Destruição de caixas de água elevadas, monumentos, casas de adobes. Danos severos a moderados em estruturas de alvenaria, obras de irrigação e diques.
   IX. Solo rachado como “crateras de areia”. Destruição de alvenaria. Danos severos a moderados em algumas estruturas de concreto armado e tubulações subterrâneas.
   X. Desabamentos. Danos severos a moderados em pontes, túneis, barragens e ferrovias.
   XI. Distúrbios permanentes no solo.
   XII. Danos quase totais.

➤ A magnitude de um terremoto é uma medida quantitativa relacionada com a energia por ele liberada. Essa energia é calculada em função da amplitude máxima dos deslocamentos registrados em sismógrafos.
Um sismógrafo é um aparelho que tem como objetivo gravar com exatidão o movimento do chão durante um terremoto. Ele contém uma agulha extremamente sensível a trepidações, que registra as vibrações do solo numa folha de papel contínua.


Imagem extraída do site InfoEscola. (Acesso em 02/02/2024.)

Quando ocorre uma vibração, o sismógrafo desenha um gráfico de ondas chamado sismograma; é a partir dos dados registrados nesse gráfico que a magnitude de um sismo é calculada.


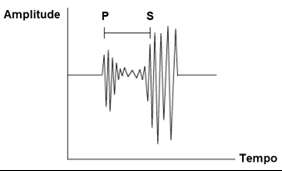
Imagem extraída de Terremotos e logaritmos . (Acesso em 02/02/2024.)

Na imagem acima, o ponto P refere-se às primeiras ondas que chegam ao epicentro (ponto da superfície terrestre no qual o tremor tem máxima magnitude), seguidas das ondas secundárias no ponto S. A Amplitude é a “altura” da onda, ou seja, a distância entre o eixo da onda e sua crista – ponto mais alto (ou o seu vale – ponto mais baixo). Quanto maior for a amplitude, maior será a quantidade de energia transportada e mais forte o terremoto.
A unidade utilizada para descrever a amplitude das ondas registradas pelo sismógrafo é o micrômetro [tex](\mu\ m)[/tex]. Como o prefixo micro, neste caso, significa [tex]10^{-6}[/tex], um micrômetro equivale a uma milionésima parte do metro. A unidade utilizada para descrever as frequências – ou a quantidade de ocorrências do fenômeno por unidade de tempo – é o Hertz [tex] (Hz).[/tex]
A cada dia, os sismógrafos acusam cerca de 500 mil eventos no planeta – 100 mil deles com magnitude acima de [tex]2[/tex] pontos na escala Richter, o suficiente para serem sentidos, mas somente alguns podendo ocasionar estragos maiores.

O que é a Escala Richter?

A escala mais conhecida para se determinar a magnitude de um terremoto é a escala Richter, conhecida oficialmente como escala de magnitude local. Ela foi desenvolvida pelos pesquisadores do Instituto de Tecnologia da Califórnia Charles Francis Richter e Beno Gutemberg, em 1935, para medir a força de um tremor e expressá-la em um número que indique sua magnitude relativa.
Richter definiu que um tremor de magnitude [tex]0,0[/tex] induz uma amplitude de deslocamento igual a [tex]1[/tex] micrômetro [tex](10^{-6}\ m)[/tex] em um sismograma obtido a [tex]100\ km[/tex] de distância do epicentro.
As medições utilizam uma escala logarítmica na base [tex]10[/tex]; assim, aumentar [tex]1,0[/tex] na escala significa que a amplitude do movimento registrado é [tex]10[/tex] vezes maior que a amplitude do movimento correspondente à unidade anterior. Por exemplo, um tremor de magnitude [tex]5,0[/tex] na escala Richter é dez vezes maior que um medindo [tex]4,0[/tex], além de liberar [tex]31,6[/tex] vezes mais energia cinética.

Atualmente, já se conhece tremores com magnitude inferior a 0,0 e, embora a escala Richter seja frequentemente citada nos meios de comunicação, na maior parte das medições ela foi substituída pela Escala de Magnitude de Momento (abreviada por MMS – Moment Magnitude Scale). Esta escala foi criada por Thomas C. Haks e Hiroo Kanamori, também pesquisadores da California Institute of Technology (Caltech), e introduzida em 1979. Ela igualmente possui um crescimento logarítmico de base [tex]10.[/tex]
Enquanto que a escala de Richter foi concebida para quantificar a energia liberada por um sismo de magnitudes entre 2,0 e 6,9, a escala de magnitude de momento é aplicável a todos os tamanhos de terremotos, mas sobretudo para ponderar a energia liberada em sismos de magnitude superior a 6,9. As duas escalas coincidem até valores de 6,9.
A tabela abaixo mostra as magnitudes dos terremotos, os efeitos causados e a frequência desses abalos.

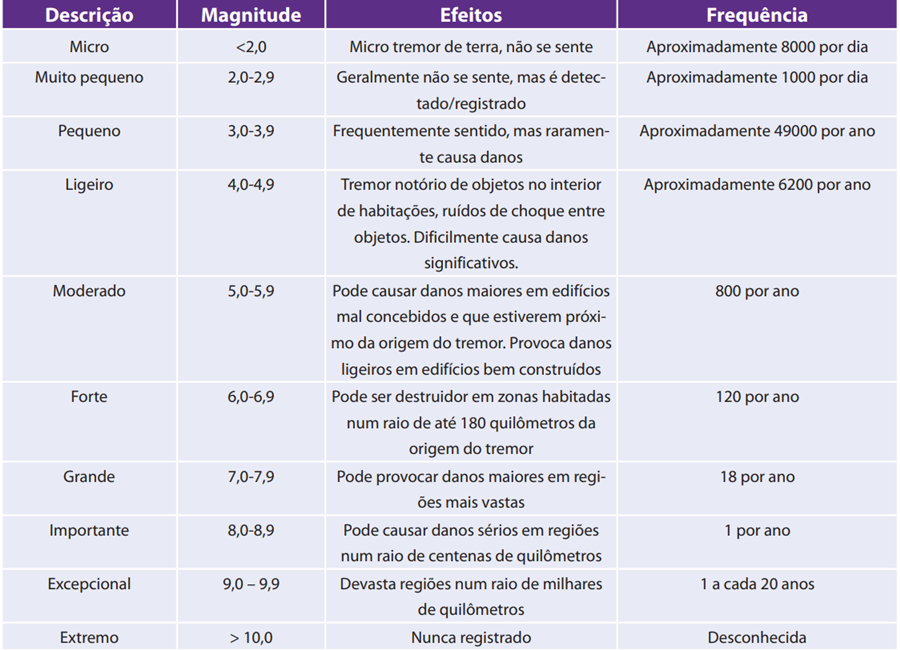
Mas como calcular a magnitude de um terremoto?

As três letrinhas vermelhas que parecem nas fórmulas acima indicam o objeto matemático logaritmo. Portanto, se quisermos calcular magnitudes de terremotos, precisamos antes saber o que é um logaritmo e conhecer suas propriedades básicas.

Então, vamos estudar um pouco sobre logaritmos?

Um pouco da Matemática dos logaritmos

Já deu para entender que os logaritmos são extremamente importantes no estudo dessa área do conhecimento humano. Por hora, faremos uma abordagem sintética do assunto e depois faremos diversas aplicações dos logaritmos ao estudo dos terremotos.

Exemplos:
● [tex]log_{2}8=3[/tex], pois [tex]2^3=8.[/tex]
● [tex]log_{3}81=4[/tex], pois [tex]3^4=81.[/tex]

Observação: Quando a base do logaritmo é [tex]10[/tex], utilizamos a seguinte notação: [tex]log_{10}x=log\ x.[/tex]

Resultados Importantes

Como consequências da definição, obedecidas as condições “[tex]a, b, c \gt 0[/tex] e [tex]a \neq 1[/tex]”, temos os seguintes resultados importantes sobre logaritmos:
(a) [tex]\boxed{log_{a}1=0}[/tex], pois [tex]a^0=1.[/tex]

(b) [tex]\boxed{log_{a}a=1}[/tex], pois [tex]a^1=a.[/tex]

(c) [tex]\boxed{log_{a}b=log_{a}c \iff b=c\,}.[/tex]
Prova:
De fato, é claro que, se [tex]b=c[/tex], então [tex]log_{a}b=log_{a}c.[/tex]
Por outro lado, se [tex]log_{a}b=log_{a}c=x[/tex], temos [tex]a^x=b[/tex] e [tex]a^x=c[/tex], donde [tex]b=c.[/tex]

(d) [tex]\boxed{log_{a}a^r=r, \forall r \in \mathbb{R}\,}.[/tex]
Prova: Seja [tex]log_{a}a^r=x[/tex]. Vamos mostrar que [tex]r=x[/tex] e, para isso, observe que:
[tex]\qquad log_{a}a^r=x \iff a^x=a^r \iff x=r.[/tex]

(e) [tex]\boxed{a^{log_{a}b}=b\,}.[/tex]
Prova: Seja [tex]a^{log_{a}b}=x[/tex]. Aqui vamos mostrar que [tex]x=b[/tex].
De fato, usando a notação [tex]log_{a}b=y[/tex], segue que [tex]a^{log_{a}b}=a^y.[/tex]
Como [tex]log_{a}b=y[/tex], pela definição de logaritmo, segue que [tex]a^y=b[/tex].
Desta forma, conclui-se que [tex]x=b.[/tex]

(f) [tex]\boxed{log_{a}(b \cdot c)= log_{a}b+ log_{a}c\,}.[/tex] (Logaritmo do produto)
Prova: Se [tex]log_{a}b=x,~ log_{a}c=y~[/tex] e [tex]~log_{a}(b \cdot c)=z[/tex], vamos mostrar que [tex]~z=x+y~.[/tex] Para isso, note que:
[tex]\qquad log_{a}b=x \iff a^x=b;[/tex]
[tex]\qquad log_{a}c=y \iff a^y=c;[/tex]
[tex]\qquad log_{a}(b \cdot c)=z \iff a^z=b \cdot c;[/tex]
assim,
[tex]\qquad a^z=b \cdot c=a^x \cdot a^y=a^{x+y}.[/tex]
Como [tex]a^z=a^{x+y}[/tex], podemos concluir que [tex]z=x+y.[/tex]
Observação: Usando uma técnica matemática chamada indução, é possível provar que essa propriedade pode ser estendida para um produto com mais de dois fatores, ou seja

(g) [tex]\boxed{log_{a}\left(\dfrac{b}{c}\right)= log_{a}b- log_{a}c~}.[/tex] (Logaritmo do quociente)
Prova: Sendo [tex]~log_{a}b=x,~log_{a}c=y~[/tex] e [tex]~log_{a}\left(\dfrac{b}{c}\right)=z[/tex], vamos mostrar que [tex]z=x-y[/tex].
De fato, observe inicialmente que:
[tex]\qquad log_{a}b=x \iff a^x=b;[/tex]
[tex]\qquad log_{a}c=y \iff a^y=c;[/tex]
[tex]\qquad log_{a}\left(\dfrac{b}{c}\right)=z \iff a^z=\dfrac{b}{c};[/tex]
então, segue que:
[tex]\qquad a^z=\dfrac{b}{c}=\dfrac{a^x}{a^y}=a^{x-y}.\\
~~[/tex]
Portanto, [tex]a^z=a^{x-y}[/tex], donde concluímos que [tex]z=x-y.[/tex]
Importante observar que, se [tex]b=1[/tex], temos:
[tex]\qquad log_{a}\left(\dfrac{1}{c}\right)= log_{a}1- log_{a}c[/tex],
ou seja, [tex]\boxed{log_{a}\left(\dfrac{1}{c}\right)=-log_{a}c~}.[/tex]

(h) [tex]\boxed{log_{a}b^r= r \cdot log_{a}b~}[/tex], para [tex] r \in \mathbb{R}.[/tex] (Logaritmo da potência)
Prova: Se [tex]log_{a}b=x~[/tex] e [tex]~log_{a}b^r=y[/tex], mostraremos que [tex]y=r \cdot x[/tex].
De fato, veja que
[tex]\qquad log_{a}b=x \iff a^x=b \iff (a^x)^r=(b)^r \iff a^{x \cdot r}=b^r[/tex]
e
[tex]\qquad log_{a}b^r=y \iff a^y=b^r.[/tex]
Assim, [tex]a^y=a^{x \cdot r}[/tex], donde [tex]y= x \cdot r.[/tex]
É importante observar que para [tex]0\lt a \neq 1, b \in \mathbb{R^+}[/tex] e [tex]n \in \mathbb{N}[/tex], temos:
[tex]\qquad log_{a}\sqrt[n]{b}=log_{a}b^{1/n}=\dfrac{1}{n} \cdot log_{a}b[/tex],
isto é, [tex]\boxed{log_{a}\sqrt[n]{b^~}=\dfrac{1}{n} \cdot log_{a}b\,}.[/tex]

(i) Mudança de base
Considere que tenhamos [tex]log_{a}b[/tex] e queremos mudar para a base [tex]k[/tex].
Sabemos, pela definição de logaritmos, que [tex]log_{a}b=y \iff a^y=b[/tex].
Aplicando logaritmo de base [tex]k[/tex] a ambos os membros da igualdade [tex]a^y=b[/tex], segue que:
[tex]\qquad a^y=b\\
\qquad log_{k}a^y= log_{k}b \\
\qquad y \cdot log_{k}a= log_{k}b \\
\qquad y=\dfrac{log_{k}b}{log_{k}a}.[/tex]
Finalmente, [tex]\boxed{log_{a}b=\dfrac{log_{k}b}{log_{k}a}}.[/tex]

Fechando a discussão

O vídeo abaixo contém e detalha várias informações que foram apresentadas nesta Sala.
Você vai saber, principalmente, de onde vêm as informações usadas para se chegar no número de magnitude: o que são ondas sísmicas e como essas ondas são medidas com um sismógrafo.

Atividades

Vamos praticar um pouco e resolver alguns problemas?
– É só clicar no botão abaixo e ir para a Sala de Atividades.

B O A    D I V E R S Ã O ! ! !

Se necessário, na Sala de Atividades você encontrará um link para voltar para esta Sala, na parte inferior à direita da página.

Equipe COM – OBMEP