Os ângulos internos de um pentágono regular
Nesta sala, vamos calcular a medida em graus dos ângulos internos de um pentágono regular. Mas quais são as informações básicas sobre os pentágonos regulares?
- Um pentágono regular é equilátero, ou seja, os lados de um pentágono regular têm o mesmo comprimento.
- Um pentágono regular é equiângulo, ou seja, os ângulos internos de um pentágono regular têm a mesma medida.
- Um pentágono regular é inscritível a uma circunferência , ou seja, existe uma única circunferência que passa pelos seus cinco vértices.
A soma das medidas dos ângulos internos de um triângulo qualquer é [tex]180^\circ.[/tex]
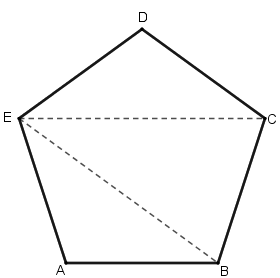Considere um pentágono regular [tex]ABCDE[/tex].
(1) Trace as diagonais [tex]\overline{EB} \, [/tex] e [tex] \, \overline{EC}.[/tex]
Observe que, com isso, decompusemos o pentágono em três triângulos:
- triângulo [tex]ABE [/tex]
- triângulo [tex]BCE [/tex]
- triângulo [tex]CDE [/tex].
Dessa forma, a soma das medidas dos ângulos internos do pentágono é exatamente a soma das medidas dos ângulos internos desses três triângulos, ou seja, [tex]\boxed{3\times 180^\circ=540^\circ} \, .[/tex]
Você pode visualizar a decomposição do passo (1) utilizando o applet abaixo. Para isso é só esperar o aplicativo carregar completamente e clicar sucessivamente nos quadradinhos que irão aparecer.
Para retornar à configuração inicial, clique nas setinhas que aparecem no canto superior do aplicativo.
OBMEP_srg, criado com o GeoGebra
(2) Como o pentágono é regular, os seus cinco ângulos internos têm a mesma medida, logo, ficou fácil determinar a medida em graus de cada ângulo interno; basta dividir [tex]540^\circ[/tex] por [tex]5[/tex]:
[tex]\qquad \qquad \dfrac{540^\circ}{5}=108^\circ.[/tex]
Assim, a medida em graus de cada ângulo interno de um pentágono regular é [tex] \, \fcolorbox{black}{#eee0e5}{$108^\circ$} \, .[/tex]
Vamos apresentar uma segunda justificativa para o valor da medida dos ângulos internos de um pentágono regular.
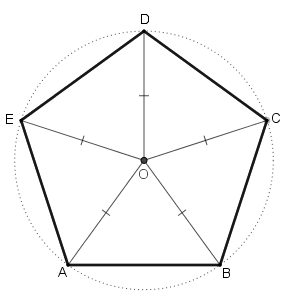Para tanto, a partir do centro do pentágono regular [tex]ABCDE[/tex], trace os segmentos [tex]\overline{OA} \, [/tex],[tex] \, \overline{OB} \, [/tex],[tex] \, \overline{OC} \, [/tex],[tex] \, \overline{OD} \, [/tex],[tex] \, \overline{OE}.[/tex] (Na verdade, esses segmentos são raios da circunferência circunscrita ao pentágono.)
Observe que agora decompusemos o pentágono em cinco triângulos isósceles congruentes:
- triângulo [tex]AOB[/tex]
- triângulo [tex]BOC[/tex]
- triângulo [tex]COD[/tex]
- triângulo [tex]DOE[/tex]
- triângulo [tex]EOA.[/tex]
Como esses cinco triângulos são congruentes, os cinco ângulos com vértices em [tex]O[/tex] têm a mesma medida:[tex]\dfrac{360^\circ}{5}=72^\circ.[/tex]
Mais do que isso: como os cinco triâgulos são isósceles, os dois outros ângulos de cada triângulo têm a mesma medida, digamos [tex]\alpha.[/tex]
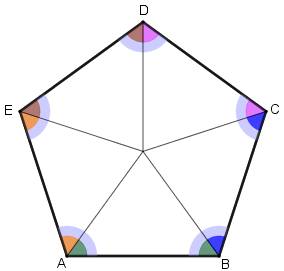
Dessa forma, a medida [tex]\alpha[/tex] dos ângulos da base de cada triângulo da decomposição do pentágono pode ser assim calculada, se utilizarmos uma vez mais que a soma das medidas dos ângulos internos de um triângulo qualquer é [tex]180^\circ[/tex]:
[tex]\qquad \alpha= \dfrac{180^\circ-72^\circ}{2}=54^\circ.[/tex]
Finalmente, como a medida de cada ângulo interno do pentágono [tex]ABCDE[/tex] é o dobro da medida dos ângulos da base dos triângulos que decompõem o pentágono, essa medida é dada por [tex] \, \fcolorbox{black}{#eee0e5}{$2 \times 54^\circ=108^\circ$} \, .[/tex]
Você pode visualizar a decomposição descrita nesta segunda justificativa, utilizando o próximo applet . Para isso é só esperar o aplicativo carregar completamente e clicar sucessivamente nos quadradinhos que irão aparecer.
Para retornar à configuração inicial, clique nas setinhas que aparecem no canto superior do aplicativo.
OBMEP_srg, criado com o GeoGebra
Equipe COM – OBMEP