.Sala de ajuda: Medindo um arco

Medindo um arco

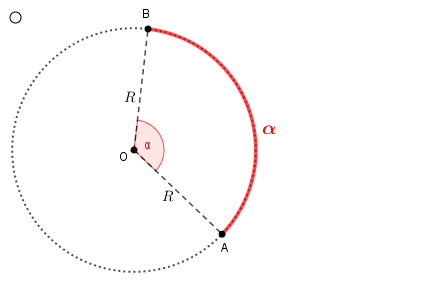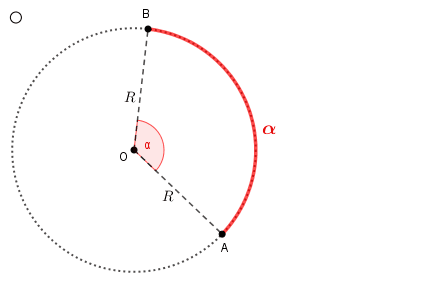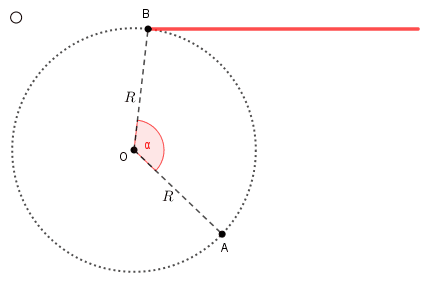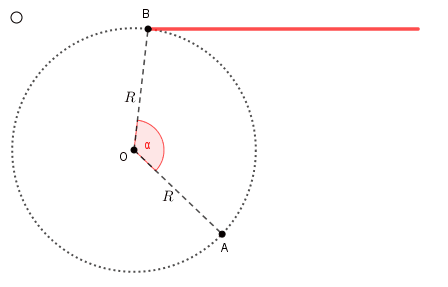
A um arco de circunferência podemos associar duas medidas distintas: uma angular e uma linear.
✐ A medida angular de um arco de circunferência é a medida do ângulo central associado a esse arco.
✐ A medida linear de um arco de circunferência é o comprimento do segmento que corresponde ao arco "esticado".

Vamos fixar o grau como medida de ângulos.
Como a própria circunferência tem uma medida angular ($360^\circ$) e uma linear ($2\pi R$), as medidas angular e linear de um arco se relacionam segundo uma regra de três simples, a partir das medidas relativas à circunferência que define o arco.
Assim, se um arco $\stackrel{\frown}{AB}$ de uma circunferência de raio $r$ tem medida angular $\alpha$, então o comprimento $c$ desse arco (medida linear) pode ser obtido pela regra de três simples assim indicada:

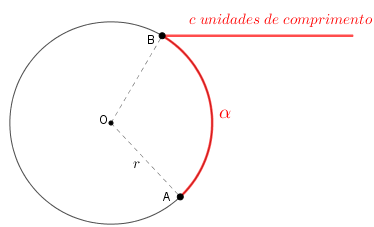
Observem que essas duas medidas são diretamente proporcionais (arcos com medidas angulares maiores têm comprimentos maiores). Assim, a proporção a ser considerada nos cálculos a serem efetuados é $\boxed{\dfrac{2\pi r}{c}=\dfrac{360^\circ}{\alpha}}$, ou ainda, $\boxed{\dfrac{c}{2\pi r}=\dfrac{\alpha}{360^\circ}}.$