Problema
(Indicado a partir do 9º ano do E. F.)
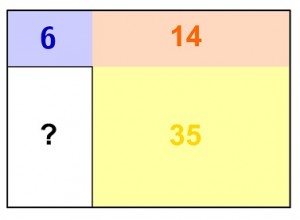
Dividimos um retângulo em quatro outros retângulos com os lados paralelos aos lados do retângulo maior, conforme indica a figura.
Se as áreas de três desses quatro retângulos são como as indicadas pela figura, qual a área do quarto retângulo?
Solução 1

Pela figura, temos que:
- [tex]a \cdot b=6[/tex]; (I)
- [tex]b \cdot c=14[/tex]; (II)
- [tex]d \cdot c=35[/tex]. (III)
Multiplicando as equações (I) e (III) obtemos que:
[tex]\qquad \qquad a \cdot b \cdot c \cdot d= 210[/tex].
Por (II):
[tex]\qquad \qquad b \cdot c=14[/tex].
Logo
[tex]\qquad \qquad a \cdot d \cdot 14=210[/tex]
[tex]\qquad \qquad a \cdot d= 15[/tex].
Portanto a área procurada é 15.
Solução elaborada pelo COM Os Nóbregas.
Solução 2
Sejam [tex]x[/tex], [tex]y[/tex], [tex]a[/tex] e [tex]b[/tex] como indicados abaixo.
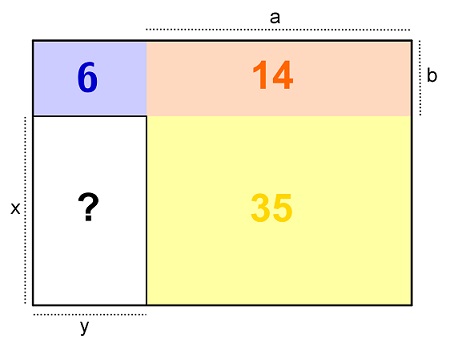
Note que, nesse caso, temos:
- [tex]y \cdot b = 6[/tex];
- [tex]a \cdot b = 14[/tex];
- [tex]a \cdot x = 35[/tex].
Multiplicando todas expressões do lado esquerdo e todos valores do lado direito, obtemos:
[tex]\qquad \qquad a^2 \cdot b^2 \cdot x \cdot y = (a \cdot b)^2 \cdot x \cdot y = 6 \cdot 14 \cdot 35[/tex]
Como [tex]a \cdot b = 14[/tex], então
[tex]\qquad \qquad x \cdot y = \dfrac{6 \cdot 14 \cdot 35}{14 \cdot 14}=15[/tex],
que é justamente a área procurada.
Solução elaborada pelos Moderadores do Blog.
