Problema
(Indicado a partir do 3º ano do E. M.)
Gira-se um triângulo acutângulo escaleno em torno de um dos seus lados, obtendo-se um sólido.
Qual deve ser o lado escolhido para que o volume do sólido seja máximo?
Solução
A princípio, considere a revolução de um triângulo de lados medindo [tex]a, b[/tex] e [tex]c[/tex] em torno de um dos lados, digamos o lado de medida [tex]a[/tex].
O sólido obtido é a união de dois cones circulares de mesma base: um com geratriz medindo [tex]b[/tex] e o outro com geratriz medindo [tex]c[/tex] (conforme ilustra a figura abaixo). O raio da base será a altura do triângulo relativa ao lado de medida [tex]a[/tex], cuja medida indicaremos por [tex]h[/tex].
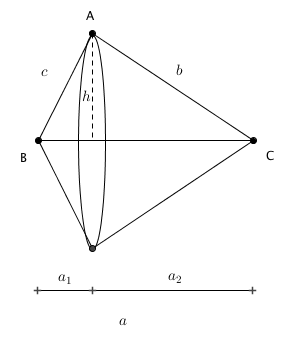
Assim, o volume do sólido é dado por
[tex]\qquad V = V_{Cone_1} + V_{Cone_2}\\
\qquad V = \dfrac{1}{3} \cdot \pi \cdot h^2 \cdot a_1 + \dfrac{1}{3} \cdot \pi \cdot h^2 \cdot a_2\\
\qquad V = \dfrac{1}{3} \cdot \pi \cdot h^2 \cdot (a_1 + a_2)\\
\qquad V = \dfrac{1}{3} \cdot \pi \cdot h^2 \cdot a[/tex]
Como [tex]a \cdot h[/tex] indica o dobro da área [tex]S[/tex] do triângulo, temos [tex]V = \dfrac{2 \pi S}{3} h[/tex].
Assim, o volume será máximo quando a altura for máxima, o que ocorre quando o lado tiver medida mínima (veja o problema Alturas do triângulo, clicando AQUI).
Solução elaborada pelos Moderadores do Blog.
Lembrete amigo:
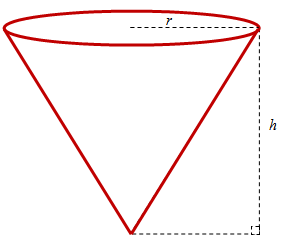
O volume de um cone circular reto com altura [tex]h[/tex] e raio da base [tex]r[/tex] é dado por:
[tex]\quad Volume=\dfrac{\acute{a}rea \, da \, base \times altura}{3}\\
\quad Volume=\dfrac{\left( \pi \cdot r^2 \right) \cdot h}{3}\\
\quad \boxed{Volume=\dfrac{\pi \cdot r^2 \cdot h}{3}}[/tex]
