Problema
(Indicado a partir do 2º ano do E. M.)
De quantos modos podemos colocar oito torres de cores diferentes num tabuleiro de xadrez, sem que uma esteja atacando outra?
Solução 1
Considere 8 torres: T1; T2; T3; T4; T5; T6; T7; T8.
- Para T1, temos 64 possibilidades de casas ( todo o tabuleiro ).
- Para T2, temos 49 possibilidades, já que desconsideramos a coluna e a linha de T1.
- Para T3, temos 36 possibilidades.
- Para T4, temos 25 possibilidades.
- Para T5, temos 16 possibilidades.
- Para T6, temos 9 possibilidades.
- Para T7, temos 4 possibilidades.
- Para T8, temos 1 possibilidade.
Portanto a quantidade de maneiras de se colocar as torres será o produto dessas possibilidades:
[tex]\qquad 64 \cdot 49 \cdot 36 \cdot 25 \cdot 16 \cdot 9 \cdot 4 \cdot 1 = 1\,625\,702\,400[/tex].
Solução elaborada pelo COM KHÉRIMA .
Solução 2
- A primeira torre pode ser colocada em qualquer uma das 64 casas do tabuleiro.
- Feito isso, a primeira torre estará atacando as casas da linha e da coluna em que se encontra. Daí restam 64 – 15 = 49 casas sem serem atacadas, então a segunda torre pode ser colocada em qualquer uma delas.
(A figura a seguir ilustra uma possível posição da primeira torre e as respectivas 15 casas nas quais a segunda torre não poderá ser colocada.)
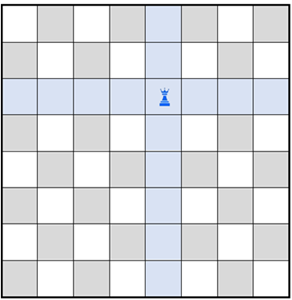
- Colocada a segunda torre, esta estará atacando as casas da linha e da coluna em que se encontra, ou seja, ela estará atacando 13 novas casas, restando 49 – 13 = 36 casas sem serem atacadas por nenhuma das duas torres já colocadas, nas quais a terceira torre poderá ser colocada.
(A partir da figura anterior, a próxima imagem ilustra uma possível posição para a segunda torre e as respectivas 15+13=28 casas nas quais a terceira torre não poderá ser colocada.)
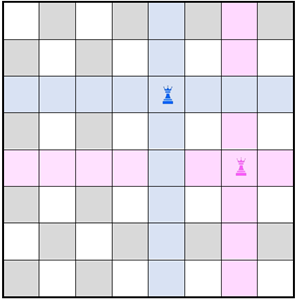
- A partir daí, é fácil perceber que a terceira torre pode ser colocada de 36 modos, a quarta de 25, a quinta de 16, a sexta de 9, a sétima de 4 e a oitava na casa restante.
(Na próxima figura, é possível observar quatro possíveis colocações de torres, as respectivas casas atacadas e, consequentemente, as 16 casas nas quais a quinta torre poderia ser colocada.)
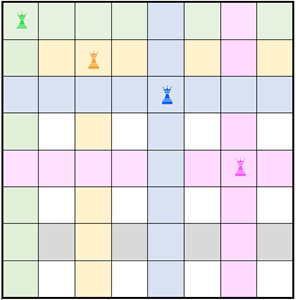
Logo, o total de modos de se colocar as 8 torres no tabuleiro, sem que uma ataque outra, é:
64 x 49 x 36 x 25 x 16 x 9 x 4 x 1 = 1 625 702 400 modos.
Solução elaborada pelos Moderadores do Blog.
Participou da discussão o Clube: KHÉRIMA.
