Problema
(Indicado a partir do 1º ano do E. M.)
Um número hexagonal centrado é um número figurado que pode ser representado por um hexágono com um ponto no centro e todos os outros pontos formando camadas hexagonais ao redor do centro.
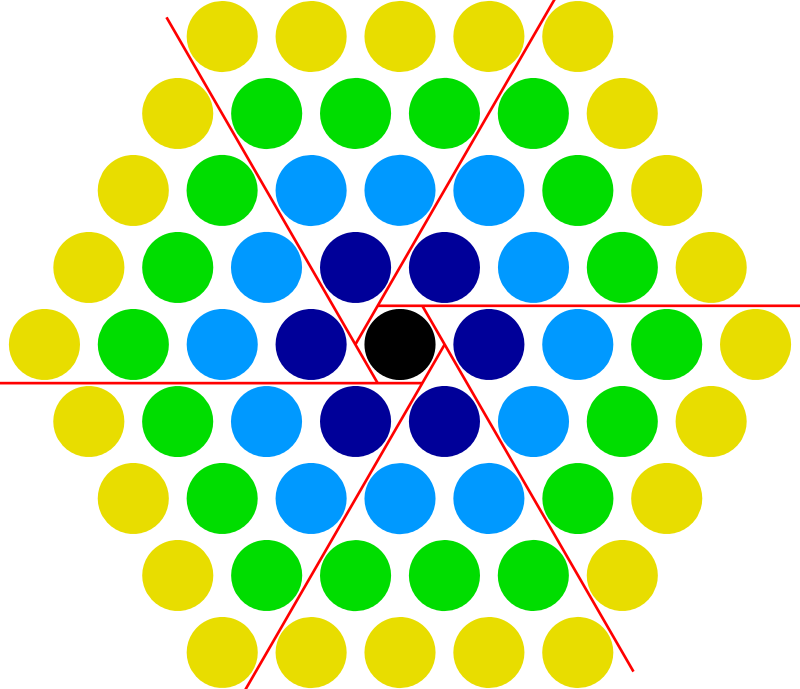
Número hexagonal centrado, Wikipedia (última visita 11 agosto 2025).
A sequência numérica [tex](1, 7, 19, \dots) [/tex] é conhecida como sequência dos números hexagonais centrados. Com a notação [tex]H_n[/tex] para o valor do termo que ocupa a posição [tex]n[/tex], pode ser provado que, para todo natural [tex]n\geq 1[/tex],
[tex]\qquad{H_{n+1}=H_{n}+6n.}[/tex]
Encontre o valor de [tex]H_{100}[/tex].

Lembrete
A soma dos [tex]n[/tex] primeiros termos da progressão aritmética [tex]\left(a_1,a_2,a_3,\cdots, a_n\right)[/tex] de razão [tex]r[/tex] é dada por [tex]\boxed{S_n=\dfrac{(a_1+a_n)}{2}\cdot n} \, .[/tex]
Solução
Aplicando repetidas vezes a fórmula de recorrência presente no enunciado da questão, obtemos
[tex]\qquad{H_{100}=H_{99}+6\cdot 99=H_{98}+6\cdot 98+6\cdot 99=H_1+6\cdot 1 +6\cdot 2 +\cdots +6\cdot 98 +6\cdot 99.}[/tex]
Observe que
[tex]\qquad{6\cdot 1 +6\cdot 2 +\cdots +6\cdot 98 +6\cdot 99=\dfrac{(6+6\cdot 99)\cdot 99}{2}=29700},[/tex]
por se tratar da soma dos [tex]99[/tex] primeiros termos de uma progressão aritmética com primeiro termo igual a [tex]6[/tex] e razão também igual a [tex]6[/tex]. Assim,
[tex]\qquad{H_{100}=H_1+29700=1+29700=29701.}[/tex]
Solução elaborada pelos Moderadores do Blog.
