Problema
(Indicado a partir do 3º ano do E. M.)
É possível resolver no plano cartesiano uma equação do segundo grau [tex]ax^2+bx+c=0[/tex], [tex]a\neq 0[/tex], utilizando um compasso.
- Basta traçar uma circunferência com centro em [tex]\left(\dfrac{-b}{2a}\,,\, \dfrac{c+a}{2a}\right)[/tex] e passando pelo ponto [tex](0,1)[/tex]. As raízes reais da equação do segundo grau são as abscissas dos pontos de interseção desta circunferência com o eixo [tex]x[/tex].
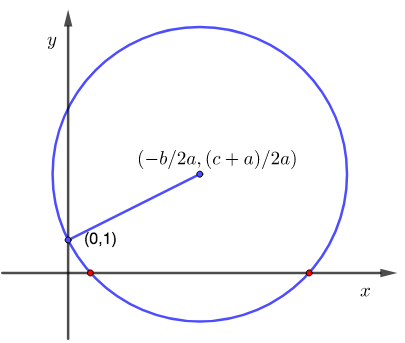
Prove que este método funciona sempre.
Fonte: Enciclopedia Matemática Mega, Tomo II.

Ajuda
Equação da circunferência
Se em um plano cartesiano [tex]xOy[/tex] o centro [tex]C[/tex] de uma circunferência [tex]\lambda[/tex] de raio [tex]r[/tex] tem coordenadas [tex](a,b)[/tex], então essa circunferência é definida algebricamente pela equação
- [tex]\boxed{\lambda:\,\left(x-a\right)^2+\left(y-b\right)^2 =r^2}[/tex].
Essa equação é denominada "equação reduzida" da circunferência [tex]\lambda\,.[/tex]
Desenvolvendo os quadrados que aparecem nessa equação, obtemos a chamada "equação geral" de [tex]\lambda\,.[/tex]
Solução
Considere a equação do segundo grau [tex]ax^2+bx+c=0[/tex], [tex]a\neq 0[/tex].
Primeiramente iremos encontrar a equação reduzida da circunferência construída de acordo com o método descrito no enunciado do problema.
- Observe que de acordo com o Teorema de Pitágoras, [tex]r^2[/tex] é dado por:
[tex]\qquad r^2=\left(\bigg\lvert\dfrac{-b}{2a}\bigg\rvert\right)^2+\left(\bigg\lvert\dfrac{c+a}{2a}-1\bigg\rvert\right)^2=\left(\dfrac{-b}{2a}\right)^2+\left(\dfrac{c+a}{2a}-1\right)^2\,.[/tex]
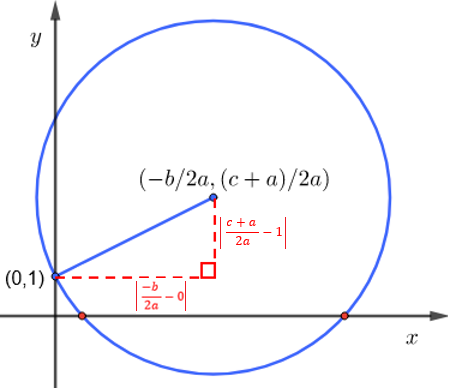
Assim, a equação reduzida da circunferência é dada por:
[tex]\qquad \left(x+\dfrac{b}{2a}\right)^2+\left(y-\dfrac{c+a}{2a}\right)^2=r^2[/tex]
[tex]\qquad \left(x+\dfrac{b}{2a}\right)^2+\left(y-\dfrac{c+a}{2a}\right)^2=\left(\dfrac{-b}{2a}\right)^2+\left(\dfrac{c+a}{2a}-1\right)^2\,.[/tex]
Desenvolvendo os quadrados que aparecem nessa equação obtemos
[tex]\, x^2+\dfrac{b}{a}x+\cancel{\dfrac{b^2}{4a^2}}+y^2-\dfrac{(c+a)}{a}y+ \cancel{\dfrac{(c+a)^2}{4a^2}}=\cancel{\dfrac{b^2}{4a^2}}+ \cancel{\dfrac{(c+a)^2}{4a^2}}-\dfrac{(c+a)}{a}+1\,[/tex]
e com algumas simplificações finalmente conseguimos a equação geral da circunferência:
[tex]\qquad x^2+y^2+\dfrac{b}{a}x-\dfrac{c+a}{a}y+\dfrac{c}{a}=0\,.[/tex]
Agora encontraremos os pontos desta circunferência que estão no eixo [tex]x[/tex], ou seja, aqueles para os quais [tex]y=0[/tex]. Substituindo esta condição na equação geral da circunferência obtemos:
[tex]\qquad x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0\,.[/tex]
Multiplicando ambos os lados por [tex]a[/tex] temos:
[tex]\qquad ax^2+bx+c=0[/tex]
e, portanto, os pontos da circunferência que estão no eixo [tex]x[/tex] possuem abscissas que são exatamente as raízes da equação inicial.
Solução elaborada pelos Moderadores do Blog.
