Problema
(Indicado a partir do 1º ano do E. M.)
Seja [tex]ABCDEFGHIJKL[/tex] um dodecágono regular inscrito numa circunferência de centro [tex]O[/tex] e raio [tex]6\text{ cm}\,.[/tex]
Mostre que o lado desse dodecágono mede [tex]3\cdot (\sqrt{6}-\sqrt{2})\text{ cm}\,.[/tex]

Lembrete para a Solução 1
Lei dos Cossenos: Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] valem as relações:
[tex]\quad {\displaystyle a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot cos{\widehat {A}}\,\!}[/tex];
[tex]\quad {\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot cos{\widehat {B}}\,\!}[/tex];
[tex]\quad {\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot cos{\widehat {C}}\,\!}[/tex].
Solução 1
Como o dodecágono é regular, cada ângulo central determinado por dois vértices consecutivos mede [tex]\dfrac{360^\circ}{12}=30^\circ\,.[/tex]
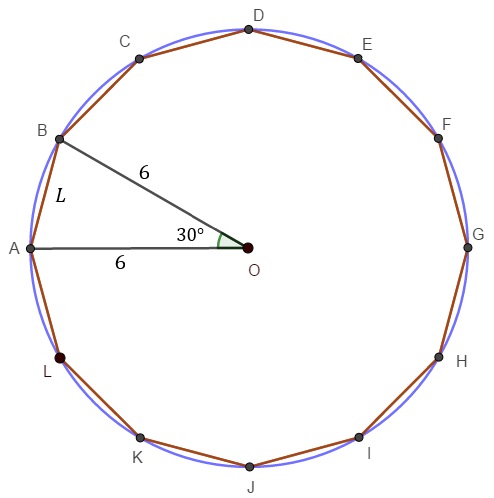
Aplicando a Lei dos Cossenos no triângulo [tex]AOB[/tex], cuja medida em centímetros do terceiro lado vamos denotar por [tex]L[/tex], segue que:
[tex]\qquad L^{2}=6^{2}+6^{2}-2\cdot 6 \cdot 6 \cdot cos 30^\circ\\
\qquad L^{2}=36+36-72 \cdot \dfrac{\sqrt{3}}{2}\\
\qquad L^{2}=36\cdot (2-\sqrt{3})\,.[/tex]
Note que [tex]L[/tex] é um número positivo, pois é a medida do lado do dodecágono, assim:
[tex]\qquad L=\sqrt{36\cdot (2-\sqrt{3})}\\
\qquad \boxed{L=6 \cdot \sqrt{2-\sqrt{3}}}\,.\qquad \textcolor{#800000}{(i)}[/tex]
Mas veja que podemos escrever [tex]\sqrt{2-\sqrt{3}}[/tex] de uma outra forma:
[tex]\qquad \begin{align*}
\sqrt{2-\sqrt{3}}&=\sqrt{\dfrac{4}{4} \cdot \left(2-\sqrt{3}\right)}\\
&=\sqrt{\dfrac{8-4\sqrt{3}}{4}}\\
&=\sqrt{\dfrac{6-2 \cdot \sqrt{6} \cdot \sqrt{2}+2}{4}}\\
&=\sqrt{\dfrac{(\sqrt{6}-\sqrt{2})^{2}}{4}}\\
&=\,\boxed{\dfrac{\sqrt{6}-\sqrt{2}}{2}}\,.
\end{align*}[/tex]
Logo, segue de [tex]\textcolor{#800000}{(i)}[/tex], que:
[tex]\qquad L=6 \cdot\dfrac{\sqrt{6}-\sqrt{2}}{2}\\
\qquad \fcolorbox{black}{#eee0e5}{$L=3 \cdot(\sqrt{6}-\sqrt{2})\text{ cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.

Lembrete e notações para a Solução 2
Algumas razões trigonométricas do ângulo notável de [tex]30^\circ[/tex]:
[tex]\qquad sen\, 30^\circ=\dfrac{1}{2}\\
\qquad cos\, 30^\circ=\dfrac{\sqrt{3}}{2}\,.[/tex]
Notações: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução 2
Como o dodecágono é regular, cada ângulo central determinado por dois vértices consecutivos mede [tex]\dfrac{360^\circ}{12}=30^\circ\,.[/tex]
Vamos construir o segmento [tex]\overline{BM}[/tex] perpendicular a [tex]\overline{AO}[/tex]. Observamos que o triângulo [tex]BMO[/tex] é retângulo de ângulos notáveis [tex]90^\circ,60^\circ,30^\circ[/tex].
Pelo lembrete, [tex]\dfrac{BM}{BO}=sen\,30^\circ=\dfrac{1}{2}[/tex], donde [tex]BM=\dfrac{BO}{2}=3[/tex].
Ainda, [tex]\dfrac{MO}{BO}=cos\,30^\circ=\dfrac{\sqrt{3}}{2}[/tex], donde [tex]MO=\dfrac{BO\sqrt{3}}{2}=3\sqrt{3}[/tex].
Logo, [tex]AM=6-3\sqrt{3}[/tex].
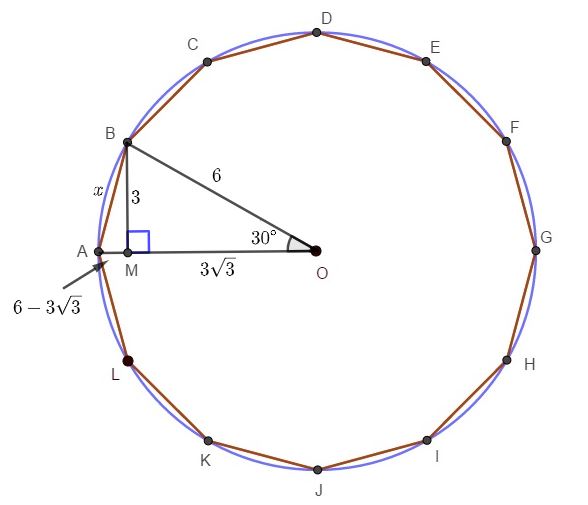
Agora, aplicando o Teorema de Pitágoras no triângulo retângulo [tex]AMB[/tex], com [tex]AB=x[/tex], segue que:
[tex]\qquad AB^{\,2}=AM^2+BM^2[/tex]
[tex]\qquad x^2=(6-3\sqrt{3})^2+3^2[/tex]
[tex]\qquad x^2=36-36\sqrt{3}+9\cdot 3+9[/tex]
[tex]\qquad x^2=72-36\sqrt3=36(2-\sqrt3)[/tex].
Como [tex]x \gt 0[/tex], então
[tex]\qquad x=\sqrt{36(2-\sqrt3)}=6\sqrt{2-\sqrt3}=3\cdot 2\sqrt{2-\sqrt3}.[/tex]
Para finalizar a questão, temos que mostrar que [tex]2\sqrt{2-\sqrt3}=\sqrt{6}-\sqrt{2}[/tex]. Como ambos os termos são positivos, basta provar que seus quadrados são iguais. Vamos lá!
Por um lado, temos que:
[tex]\qquad (2\sqrt{2-\sqrt3})^2=4(2-\sqrt3)=\boxed{8-4\sqrt3}[/tex],
e por outro, temos que:
[tex]\qquad(\sqrt{6}-\sqrt{2})^2=6-2\sqrt{12}+2=\boxed{8-4\sqrt3}[/tex],
logo, [tex](2\sqrt{2-\sqrt3})^2=(\sqrt{6}-\sqrt{2})^2[/tex], o que finaliza a questão.
Solução elaborada pelos Moderadores do Blog.
