.Problemão: Encontre o ângulo

Problema
(Indicado a partir do 8º ano do E. F.)

No triângulo $ABC$ foram marcados os pontos $D$ e $E$ sobre os lados $\overline{BC}$ e $\overline{ AC}$ , respectivamente, tais que $CD=DE=EB=BA$ .
Sabendo que o ângulo $A\widehat{C}B$ mede $20^{\circ}$ , encontre a medida do ângulo $A\widehat{D}E$ .

Lembretes

A soma das medidas dos ângulos internos de um triângulo é $180^\circ$ .
(ii) Todo triângulo isósceles possui os ângulos da base com a mesma medida.

– Denotaremos a medida do ângulo de vértice $V$ e definido por dois pontos, digamos $X$ e $Y$ , por $X\widehat{V}Y.$
– Denotaremos o segmento definido por dois pontos, digamos $X$ e $Y$ , por $\overline{XY}$ e o seu comprimento por $XY$ .

Solução

De acordo com os dados do problema, podemos ter o triângulo da figura abaixo.

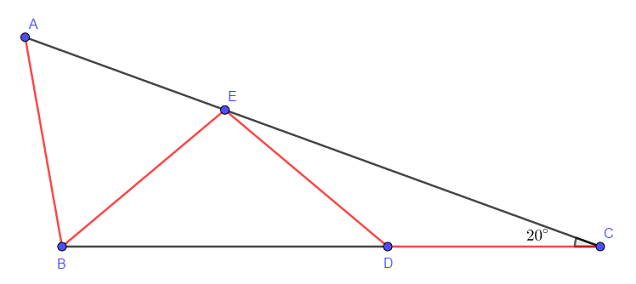
Sendo o triângulo $CDE$ isósceles, pois $CD=DE$ , pelo $\textbf{Lembrete (ii)}$ temos $D\widehat{E}C=20^{\circ}$ . Pelo $\textbf{Lembrete (i)}$ , resulta que $C\widehat{D}E=140^{\circ}$ .

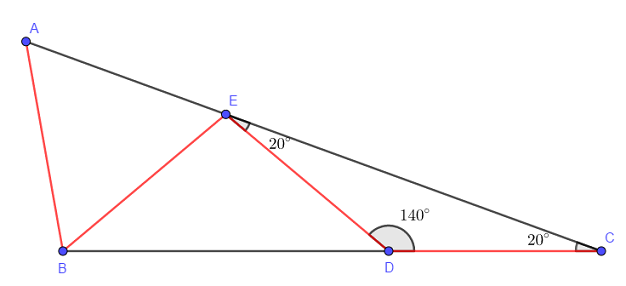
Como $B\widehat{D}C=180^{\circ}$ e o triângulo $BED$ é isósceles, pois $DE=EB$ , pelo $\textbf{Lembrete (ii)}$ obtemos que $B\widehat{D}E=D\widehat{B}E=40^{\circ}$ . Novamente, pelo $\textbf{Lembrete (i)}$ temos $B\widehat{E}D=100^{\circ}$ .

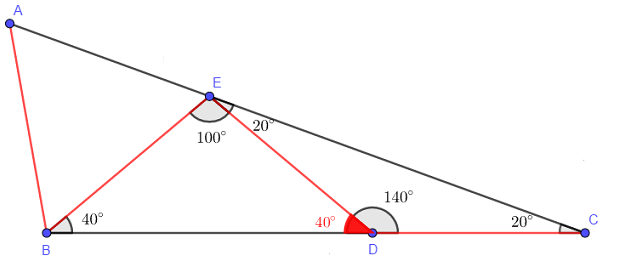
Sendo $C\widehat{E}A=180^{\circ}$ , temos que $B\widehat{E}A=60^{\circ}$ . Como o triângulo $ABE$ é isósceles, pois $EB=BA$ , pelo $\textbf{Lembrete (ii)}$ obtemos que $B\widehat{A}E=60^{\circ}$ . Pelo $\textbf{Lembrete (i)}$ temos $A\widehat{B}E=60^{\circ}$ . Notemos que o triângulo $ABE$ que é isósceles é também equilátero.

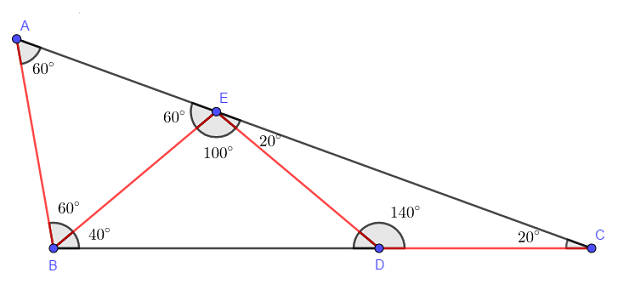
Agora, vamos considerar o triângulo $AED$ e encontrarmos a medida de $A\widehat{D}E$ .

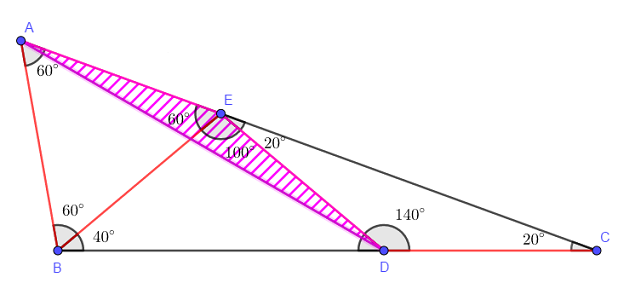
Vemos que o triângulo $AED$ é isósceles. Sendo $A\widehat{E}D=160^{\circ}$ e os ângulos $E\widehat{A}D$ e $A\widehat{D}E$ congruentes, então pelo $\textbf{Lembrete (i)}$ temos $\fcolorbox{black}{#eee0e5}{$A\widehat{D}E=10^{\circ}$}$ .

Solução elaborada pelos Moderadores do Blog.