Problema
(Indicado a partir do 1º ano do E. M.)
Um cãozinho está a [tex]10\,m[/tex] de um balão pousado no solo. O cão começa a correr em direção ao balão no mesmo instante em que este se desprende do solo e inicia uma ascensão vertical.
Se o cão corre com velocidade de [tex]2\,m/s[/tex] e o balão ascende com velocidade de [tex]1\,m/s[/tex], qual a distância mínima entre o cão e o balão? Quantos segundos após o início da corrida essa distância é mínima?
Extraído de Temas e Problemas Elementares – Elon Lages Lima et al, 2005.
Solução
- Sabendo que a distância inicial entre o cachorro e o balão é de [tex]10\,m[/tex] e que o cachorro corre a uma velocidade de [tex]2\,m/s[/tex], então a distância [tex](s)[/tex] entre o cachorro e o ponto de partida do balão pode ser escrita em função do tempo [tex](t)[/tex] como [tex]\boxed{s=10-2t}.[/tex]
- Sabemos, ainda, que o balão sobe a uma velocidade de [tex]1\,m/s[/tex]; assim, temos que a distância [tex](h)[/tex], em função do tempo [tex](t)[/tex], entre o balão e seu ponto de partida é dada por [tex]\boxed{h=t}.[/tex]
Como o cachorro corre horizontalmente e o balão sobe verticalmente, podemos representar essa situação utilizando um triângulo retângulo, cujos catetos são a “distância entre o cachorro e o ponto de partida do balão” e a “distância do balão ao solo”. A hipotenusa será a distância entre o cachorro e o balão, que vamos chamar de [tex]d[/tex].
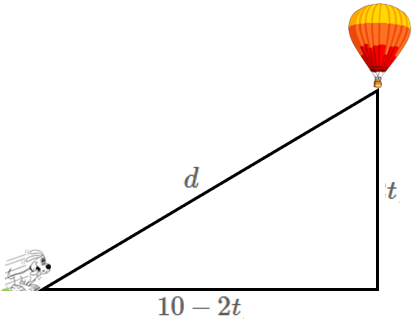
Assim, pelo Teorema de Pitágoras, [tex]d^2=(10-2t)^2 + t^2[/tex] e, portanto, [tex]d = \sqrt{(10-2t)^2+t^2}[/tex] (lembre-se de que [tex]d \gt 0[/tex]).
O nosso objetivo é encontrar a distância mínima entre o cachorro e o balão. Para isso, note que a função raiz quadrada, [tex]f(x)=\sqrt{x~}[/tex], é crescente; portanto, o nosso [tex]~d~[/tex] terá o valor mínimo quando o radicando [tex](10-2t)^2+t^2[/tex] for mínimo.
Mas [tex](10-2t)^2+t^2=100-40t+5t^2[/tex] e sabemos que uma relação da forma [tex]y=at^2+bt+c[/tex], com [tex]a\gt 0[/tex], descreve uma parábola com concavidade voltada para cima, no plano cartesiano [tex]tOy[/tex].
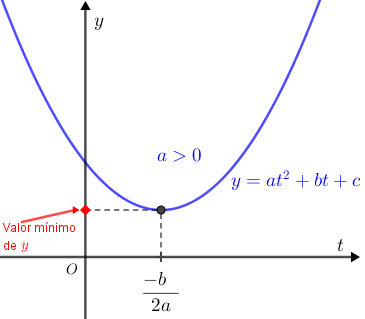
Dessa forma, a expressão [tex](10-2t)^2+t^2[/tex] terá seu valor mínimo na coordenada [tex]t[/tex] relativa ao vértice da parábola definida por [tex]y=100-40t+5t^2[/tex], ou seja, [tex]t=\dfrac{-(-40)}{2\cdot5}=4[/tex].
Substituindo, esse valor de [tex]t[/tex] em [tex]d=\sqrt{(10-2t)^2+t^2}[/tex], obtemos que a distância mínima é [tex]\fcolorbox{black}{#eee0e5}{$ 2 \sqrt{5}\, m$}\,[/tex], que ocorre após [tex]\fcolorbox{black}{#eee0e5}{$4\,s$}[/tex].
Solução enviada pelo Clube OLÍMPICOS FEDERAIS, com contribuições dos Moderadores do Blog.
