Problema
(Indicado a partir do 1º ano do E. M.)
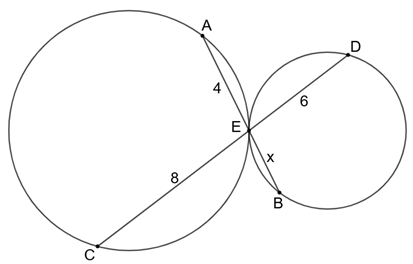
Duas circunferências tangentes estão mostradas na figura com dois segmentos [tex]\overline{AB}[/tex] e [tex]\overline{CD}[/tex] concorrentes em [tex]E[/tex], ponto de tangência das circunferências. Determine a medida [tex]x[/tex].

AJUDAS
(I) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
(II) Ângulos opostos pelo vértice têm a mesma medida.
(III) Em uma circunferência, um ângulo de segmento, ou ângulo semi-inscrito, é formado por uma corda e uma tangente, com vértice no ponto de tangência. Se um ângulo de segmento e um ângulo inscrito visualizam o mesmo arco, então eles têm a mesma medida.
Solução
Tracemos uma reta [tex]r[/tex] tangente a ambas as circunferências em [tex]E[/tex] e sejam [tex]R[/tex] e [tex]S[/tex] pontos de [tex]r[/tex]. Perceba que [tex]\angle{DBE}=\angle{DER}=\beta[/tex] (visualizam o mesmo arco) e [tex]\angle{BDE}=\angle{BES}=\alpha[/tex] (visualizam o mesmo arco). Por outro lado, [tex]\angle{CES}=\angle{DER}=\beta[/tex] (opostos pelo vértice) e [tex]\angle{BES}=\angle{AER}=\alpha[/tex] (opostos pelo vértice). Mais ainda, [tex]\angle{CES}=\angle{CAE}=\beta[/tex] (visualizam o mesmo arco) e [tex]\angle{AER}=\angle{ACE}=\alpha[/tex] (visualizam o mesmo arco).
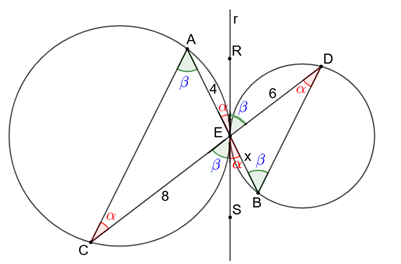
Do exposto, [tex]\triangle CEA \sim \triangle DEB[/tex] pelo caso A.A. Logo,
[tex]\qquad \dfrac{EB}{ED}=\dfrac{EA}{EC}\Rightarrow \dfrac{x}{6}=\dfrac{4}{8}\Rightarrow x=3.[/tex]
Solução elaborada pelos Moderadores do Blog.
