Problema
(Indicado a partir do 3º ano do E. M.)
No aniversário de “Triangulino”, cinco de seus amigos resolveram homenagear o companheiro com um bolo feito no formato de um prisma triangular, conforme mostrado a seguir.
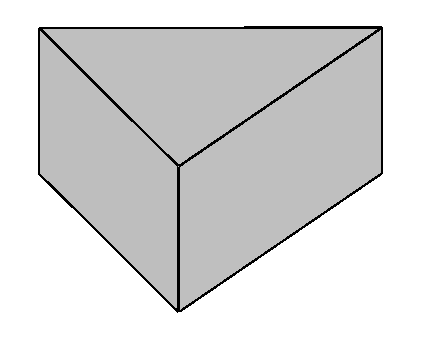
“Triangulino” resolveu dividir o bolo entre todos os presentes de modo que cada corte, feito com uma faca e de cima para baixo, passasse pelo ponto médio de cada lado do triângulo da face superior do bolo e também passasse pelo vértice oposto, conforme podemos ver na próxima figura.
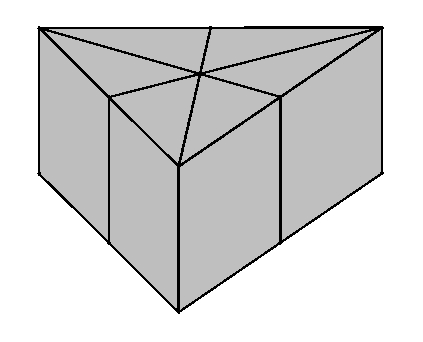
Em relação aos volumes das fatias, o que podemos afirmar? Justifique sua resposta.

Lembretes
(1) A área de um triângulo é dada por [tex]\boxed{\frac{\text{base $\times$ altura}}{2}}[/tex]. Assim, triângulos com mesma medida de base e mesma medida de altura em relação essa base, têm a mesma área.
(2) O volume de um prisma é dado por [tex]\boxed{\text{área da base $\times$ altura}}[/tex]. Logo, prismas com mesma medida de área de base e mesma medida de altura têm o mesmo volume.
Solução
Os segmentos que ligam os vértices [tex]A, B[/tex] e [tex]C[/tex] do triângulo, base do prisma, aos pontos médios dos lados opostos, que denominaremos [tex]D, E[/tex] e [tex]F[/tex], respectivamente, são chamados medianas.
Seja [tex]P[/tex] o baricentro desse triângulo (encontro das medianas). Obtém-se, então, seis triângulos [tex]BPD, CPD, APE, CPE, APF[/tex] e [tex]BPF[/tex].
Inicialmente, vamos mostrar que todos esses triângulos têm mesma área!
- Observe que os triângulos [tex]BPD[/tex] e [tex]CPD[/tex] possuem mesma área, pois têm mesma base e mesma altura em relação ao vértice [tex]P[/tex] (Lembrete [tex]1[/tex]). Chamaremos a área comum desses dois triângulos de [tex]a[/tex].
Analogamente, as áreas de [tex]APF[/tex] e [tex]BPF[/tex] são iguais e serão chamadas de [tex]b[/tex] e as áreas de [tex]APE[/tex] e [tex]CPE[/tex] também são iguais e serão chamadas de [tex]c[/tex].
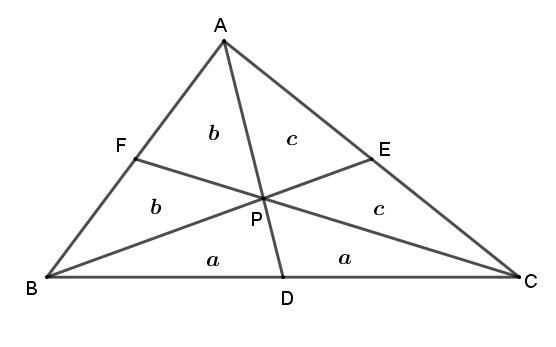
- Agora, observe que as áreas dos triângulos [tex]BAD[/tex] e [tex]CAD[/tex] também são iguais, uma vez que esses triângulos também têm mesma base e mesma altura em relação ao vértice [tex]A[/tex]. Assim, pode-se escrever:
- De forma análoga, as áreas dos triângulos [tex]CBE[/tex] e [tex]ABE[/tex] também são iguais, uma vez que esses triângulos também têm mesma base e mesma altura em relação ao vértice [tex]B[/tex]. Assim, pode-se escrever que:
[tex]\qquad a+2b=a+2c[/tex], donde
[tex]\qquad 2b=2c[/tex] e
[tex]\qquad \boxed{b=c}.[/tex]
[tex]\qquad c+2b=c+2a[/tex], donde
[tex]\qquad 2b=2a[/tex] e
[tex]\qquad \boxed{b=a} \, .[/tex]
Portanto, [tex]a=b=c[/tex] e os seis triângulos possuem mesma área.
Finalmente, pode-se concluir que, como as áreas dos seis triângulos da base são iguais e como a altura de cada fatia em relação à base do bolo é a mesma, então o volume de cada prisma assim obtido será o mesmo, pois o volume de cada prisma formado é dado pelo produto da área da base pela sua altura.
Solução elaborada pelos Moderadores do Blog.
