Problema
(Indicado a partir do 2º ano do E. M.)
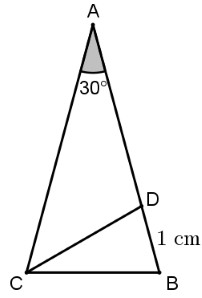
Na figura abaixo, os triângulos [tex]ABC[/tex] e [tex]BCD[/tex] são isósceles de bases [tex]\overline{BC}[/tex] e [tex]\overline{BD},[/tex] respectivamente. Encontre a área do triângulo [tex]ABC,[/tex] sabendo que [tex]BD = 1~\text{cm}.[/tex]

Lembrete
[tex]\textbf{ (Lei dos Cossenos)}[/tex] Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] valem as relações:
[tex]\quad {\displaystyle a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot cos{\widehat {A}}\,\!}[/tex];
[tex]\quad {\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot cos{\widehat {B}}\,\!}[/tex];
[tex]\quad {\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot cos{\widehat {C}}\,\!}[/tex].
Solução
O enunciado nos diz que os triângulos [tex]ABC[/tex] e [tex]BCD[/tex] são isósceles. Observe que [tex]\hat{B}[/tex] é ângulo da base desses dois triângulos e, consequentemente, esses triângulos são semelhantes.
Considere [tex]BC = l~\text{cm}.[/tex] Como os triângulos [tex]ABC[/tex] e [tex]BCD[/tex] são semelhantes, podemos aplicar a seguinte razão de semelhança:
[tex]\qquad \dfrac{AC}{CB} = \dfrac{CB}{BD}[/tex]
[tex]\qquad \dfrac{AC}{l} = \dfrac{l}{1}[/tex]
[tex]\qquad AC= l^2~\text{cm}.[/tex]
Assim, temos as medidas dos lados do triângulo [tex]ABC[/tex] em termos de [tex]l[/tex]: [tex]BC = l~\text{cm}[/tex] e [tex]AB = AC = l^2~\text{cm}.[/tex]
Agora, podemos aplicar a Lei dos Cossenos no triângulo [tex]ABC[/tex]:
[tex]\qquad BC^2 = AB^2+AC^2-2\cdot AB\cdot AC\cdot \cos 30^{\circ}[/tex]
[tex]\qquad l^2 = (l^2)^2+(l^2)^2-2\cdot l^2\cdot l^2\cdot \dfrac{\sqrt{3}}{2}[/tex]
[tex]\qquad l^2 = 2l^4- l^4\cdot \sqrt{3}[/tex]
[tex]\qquad l^2 = l^4(2-\sqrt{3})[/tex]
[tex]\qquad 1 = l^2(2-\sqrt{3})[/tex]
[tex]\qquad l^2 = \dfrac{1}{2-\sqrt{3}}[/tex]
[tex]\qquad l^2 = 2+\sqrt{3}.[/tex]
Logo, [tex]AB = AC = 2+\sqrt{3}~\text{cm}.[/tex]
Assim, representando por [tex][ABC][/tex] a área do triângulo [tex]ABC[/tex], temos
[tex]\qquad [ABC] = \dfrac{1}{2}\cdot AB\cdot AC\cdot \text{sen}~30^{\circ}[/tex]
[tex]\qquad [ABC] = \dfrac{1}{2}\cdot (2+\sqrt{3})\cdot (2+\sqrt{3})\cdot \dfrac{1}{2}[/tex]
[tex]\qquad [ABC] = \left(\dfrac{2+\sqrt{3}}{2}\right)^2[/tex]
[tex]\qquad [ABC] = \dfrac{4+2\cdot 2\cdot \sqrt{3}+3}{4}[/tex]
[tex]\qquad \boxed{[ABC] = \sqrt{3}+\dfrac{7}{4}~\text{cm}^2}.[/tex]
Solução elaborada pelos Moderadores do Blog.
