Problema
(Indicado a partir do 9º ano do E. F.)
A figura abaixo representa um retângulo [tex]ABCD[/tex] dividido em quatro triângulos.
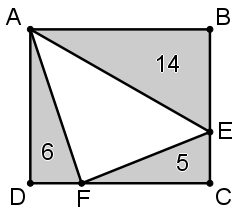
Os números nos interiores dos triângulos sombreados indicam a área, em centímetros, do respectivo triângulo.
Determine a área do triângulo [tex]AEF.[/tex]
Solução 1
Consideremos [tex]DF=x[/tex] e [tex]FC = y[/tex], Assim, [tex]AB = x+y.[/tex] Observe que os três triângulos sombreados são retângulos. Assim, suas áreas podem ser calculadas multiplicando-se os catetos e dividindo-se o resultado por 2.
Representemos a área de um triângulo [tex]XYZ[/tex] por [tex](XYZ)[/tex]. Dessa forma,
[tex]\qquad \begin{align}(ABE) = 14&\Rightarrow \dfrac{AB\times BE}{2} = 14\\
&\Rightarrow AB\times BE = 28\\
&\Rightarrow (x+y)\times BE = 28\\
&\Rightarrow \boxed{BE = \dfrac{28}{x+y}}.
\end{align}[/tex]
[tex]\qquad \begin{align}(ADF) = 6&\Rightarrow \dfrac{AD\times DF}{2} = 6\\
&\Rightarrow AD\times DF = 12\\
&\Rightarrow AD\times x = 12\\
&\Rightarrow \boxed{AD = \dfrac{12}{x}}.
\end{align}[/tex]
[tex] \qquad \begin{align}(ECF) = 5&\Rightarrow \dfrac{EC\times CF}{2} = 5\\
&\Rightarrow EC\times CF = 10\\
&\Rightarrow EC\times y = 10\\
&\Rightarrow \boxed{EC = \dfrac{10}{y}}.
\end{align}[/tex]
Veja a figura com as medidas encontradas:
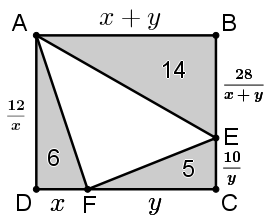
Como [tex]ABCD[/tex] é um retângulo, em particular, temos
[tex]\qquad AD=BC=BE+EC. [/tex]
Substituindo nessa última expressão as medidas destacadas, ficaremos com
[tex]\qquad \dfrac{12}{x}=\dfrac{28}{x+y}+\dfrac{10}{y}[/tex]
[tex]\qquad 12y(x+y) = 28xy+10x(x+y)[/tex]
[tex]\qquad 12xy+12y^2= 28xy+10x^2 +10xy[/tex]
[tex]\qquad 10x^2+26xy-12y^2=0.[/tex]
Note que a última igualdade pode ser vista como uma equação do 2º grau em [tex]x[/tex]. Assim, podemos resolvê-la usando a fórmula resolutiva de equações quadráticas:
[tex]\qquad x = \dfrac{-26y\pm\sqrt{(26y)^2-4\cdot 10\cdot (-12y^2)}}{2\cdot 10}[/tex]
[tex]\qquad x = \dfrac{-26y\pm\sqrt{676y^2+480y^2}}{20}[/tex]
[tex]\qquad x = \dfrac{-26y\pm\sqrt{1156y^2}}{20}[/tex]
[tex]\qquad x = \dfrac{-26y\pm 34y}{20}[/tex]
[tex]\qquad x_1 = \dfrac{-26y+ 34y}{20}[/tex] ou [tex] x_2 = \dfrac{-26y- 34y}{20}[/tex]
[tex]\qquad x_1 = \dfrac{8y}{20}[/tex] ou [tex] x_2 = \dfrac{-60y}{20}[/tex]
[tex]\qquad \boxed{x_1 = \dfrac{2y}{5}}[/tex] ou [tex] \boxed{x_2 = -3y\lt 0}.[/tex]
Como [tex]x_2\lt 0[/tex] e não existe medida de comprimento negativa, então consideramos apenas o caso em que [tex]x=\dfrac{2y}{5}.[/tex] A área do retângulo é dada por [tex](x+y)\cdot \dfrac{12}{x}[/tex] e, portanto, é igual a
[tex]\qquad \left(\dfrac{2y}{5}+y\right)\cdot \dfrac{12}{\frac{2y}{5}} = \dfrac{7y}{5}\cdot \dfrac{60}{2y} = \dfrac{7\cancel{y}}{5}\cdot \dfrac{60}{2\cancel{y}} = \dfrac{420}{10} = 42 \;\text{cm}^2.[/tex]
Logo, a área do triângulo [tex]AEF[/tex] é dada por
[tex]\qquad (AEF)=42-\left((ABE)+(ADF)+(ECF)\right) =42-(14+6+5) = 42-25 = \boxed{17\;\text{cm}^2}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Perceba que, para descobrirmos a área do triângulo [tex]AEF[/tex], podemos apenas encontrar a área do retângulo [tex]ABCD[/tex], e retirar as áreas dos demais triângulos que já sabemos. Para isso, sabendo que a área de [tex]ABCD[/tex] é dada por [tex]AB \cdot AD[/tex], vamos primeiramente tomar as seguintes igualdades:
[tex]\qquad \dfrac{AB \cdot BE}{2} = 14\Rightarrow AB \cdot BE = 28\Rightarrow \boxed{BE = \dfrac{28}{AB}}; \;\;\;(I)[/tex]
[tex]\qquad \dfrac{DF \cdot AD}{2} = 6\Rightarrow DF \cdot AD = 12\Rightarrow \boxed{DF = \dfrac{12}{AD}}; \;\;\;(II)[/tex]
[tex]\qquad \dfrac{FC \cdot CE}{2} = 5 \Rightarrow \boxed{FC \cdot CE = 10}.\;\;\;(III)[/tex]
Perceba também que:
[tex]\qquad AB = DF + FC \Rightarrow FC = AB – DF[/tex]
[tex]\qquad AD = CE + BE \Rightarrow CE = AD – BE[/tex]
Substituindo [tex]CE[/tex] e [tex]FC[/tex] na igualdade [tex](III),[/tex] temos:
[tex]FC \cdot CE = 10 \Rightarrow (AB-DF)(AD-BE) = 10 \Rightarrow (AB \cdot AD)-(AB \cdot BE)-(DF \cdot AD)+(DF \cdot BE) = 10.[/tex]
Agora, pelas áreas dos triângulos [tex]ABD[/tex] e [tex]ADF[/tex], concluímos que [tex]AB\cdot AD = 28[/tex] e [tex]DF\cdot AD=12.[/tex]
Substituindo as relações das igualdades [tex](I)[/tex] e [tex](II),[/tex] obtemos
[tex]\qquad (AB \cdot AD)-28-12 + \left(\dfrac{12}{AD} \cdot \dfrac{28}{AB}\right) = 10 \Rightarrow (AB \cdot AD) + \dfrac{336}{AB \cdot AD} = 50[/tex]
[tex]\qquad \dfrac{(AB \cdot AD)^2 + 336}{(AB \cdot AD)} = 50[/tex]
[tex]\qquad (AB \cdot AD)^2 + 336 = 50 (AB \cdot AD)[/tex]
[tex]\qquad (AB \cdot AD)^2 – 50 (AB \cdot AD) + 336 = 0.[/tex]
Com isso, chegamos a uma equação de segundo grau em [tex](AB \cdot AD)[/tex], que é o valor da área do quadrado [tex]ABCD[/tex]. Tomando [tex](AB \cdot AD) = x[/tex], encontramos as raízes [tex]x’ = 42[/tex] e [tex]x” = 8[/tex], porém, excluímos a raiz [tex]x” = 8[/tex], pois seria impossível retirarmos a área dos demais triângulos, já que resultaria em um valor negativo. Portanto, a área do quadrado [tex]ABCD[/tex], que também é igual ao produto [tex]AB \cdot AD[/tex], é de [tex]42 \ cm^2[/tex]. Logo, a área do triângulo [tex]AEF[/tex] é igual a [tex]42-14-6-5 = 17 \ cm^2.[/tex]
Solução elaborada pelo Potências de Euler, com contribuições dos Moderadores do Blog.
