Problema
(Indicado a partir do 9º ano do E. F.)
Tenho o dobro da idade que tu tinhas quando eu tinha a idade que tu tens; quando tiveres a idade que eu tenho, a soma de nossas idades será 90 anos.
Determine as idades atuais.
Extraído da RPM 08.
Solução
Vamos analisar o problema em três tempos diferentes: no passado, no presente e no futuro.
Vamos chamar as duas pessoas de A e de B, sendo A aquela que nos dá o enunciado.
- No passado: A tinha uma idade [tex]m[/tex] e B tinha uma idade [tex]n[/tex].
- Passados [tex]x[/tex] anos chegamos ao presente onde: A tem uma idade [tex]2n[/tex] e B tem uma idade [tex]m[/tex].
- Passando [tex]y[/tex] anos chegaremos ao futuro, quando A vai ter uma idade qualquer [tex]a[/tex] e B terá uma idade [tex]2n[/tex].
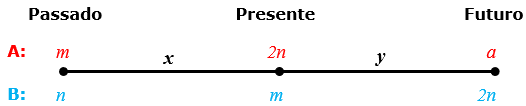
Olhando para a idade de A no passado e no presente teremos que: [tex]m+x=2n\,.[/tex]
Olhando para a idade de B no passado e no presente teremos que: [tex]n+x=m\,.[/tex]
Somando essas duas equações teremos:
[tex]\quad m+n+2x=2n+m[/tex]
[tex]\quad 2x=n[/tex]
[tex]\quad \boxed{x=n/2}.[/tex]
Substituindo o valor encontrado para [tex]x[/tex] na primeira equação, segue que:
[tex]\quad m+x=2n[/tex]
[tex]\quad m+n/2=2n[/tex]
[tex]\quad m=2n-n/2[/tex]
[tex]\quad \boxed{m=3n/2}.[/tex]
Já temos um valor para [tex]m[/tex], então podemos olhar para B no presente e no futuro; assim:
[tex]\quad m+y=2n[/tex]
[tex]\quad 3n/2+y=2n[/tex]
[tex]\quad y=2n-3n/2[/tex]
[tex]\quad \boxed{y=n/2}.[/tex]
Dessa forma, a idade de A no futuro vai ser definida por:
[tex]\quad a=2n+y[/tex]
[tex]\quad a=2n+n/2[/tex]
[tex]\quad \boxed{a=5n/2}.[/tex]
A soma das idades de A e de B no futuro deve dar [tex]90[/tex], logo:
[tex]\quad a+2n=90[/tex]
[tex]\quad 5n/2+2n=90[/tex]
[tex]\quad 9n/2=90[/tex]
[tex]\quad \boxed{n=20}.[/tex]
Como [tex]m=3n/2[/tex], então [tex]\boxed{m=30}.[/tex]
Assim, a idade atual de A é 40 anos e a de B é 30 anos.
Solução enviada pelo Clube Aprendizes dos Números , com contribuições dos Moderadores do Blog.
