Problema
(Indicado a partir do 3º ano do E. M.)
A reta [tex]r[/tex] tem equação [tex]y = 2x + 8[/tex], e intercepta o eixo [tex]y[/tex] no ponto [tex]A[/tex], e o eixo [tex]x[/tex], no ponto [tex]B[/tex].
Seja [tex]M[/tex] o ponto médio do segmento [tex]\overline{AB}[/tex] e [tex]O[/tex] a origem do sistema cartesiano, conforme imagem abaixo.
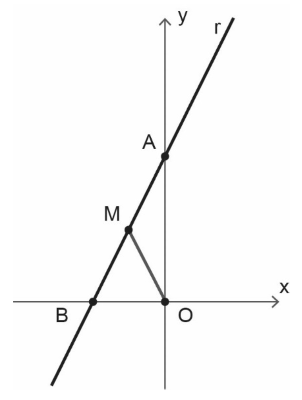
Quanto vale a área do triângulo [tex]AMO[/tex]?
Adaptado de PUC – RIO, 2022.
Solução
Observe que, como a medida da base [tex]\overline{AM}[/tex] do triângulo [tex]AMO[/tex] é igual à metade da medida da base [tex]\overline{AB}[/tex] do triângulo [tex]ABO[/tex] e as alturas relativas a essas bases são a mesma, então a área do triângulo [tex]AMO[/tex] é igual à metade da área do triângulo [tex]ABO[/tex]. Assim, precisamos encontrar primeiramente a área de [tex]ABO[/tex]. Veja que podemos calcular a área de [tex]ABO[/tex], por
[tex]\qquad Area_{ABO} = \dfrac{BO\times AO}{2}.[/tex]
A reta [tex]r[/tex] intersecta o eixo [tex]y[/tex] em [tex]x=0[/tex], ou seja, em [tex]y = 2\cdot 0+8=8[/tex], e intersecta o eixo [tex]x[/tex] em [tex]y=0[/tex], ou seja, [tex]0=2x+8\Rightarrow x = -4[/tex].
Assim, [tex]Area_{ABO} = \dfrac{4\times 8}{2}\Rightarrow Area_{ABO}=16.[/tex]
Como a área do triângulo [tex]AMO[/tex] é igual à metade da área do triângulo [tex]ABO[/tex], então [tex]Area_{AMO} = 8[/tex].
Solução elaborada pelos Moderadores do Blog.
