Problema
(Indicado a partir do 2º ano do E. M.)
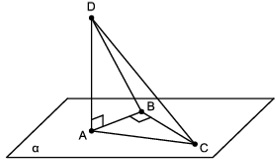
Considere um plano [tex]\alpha [/tex] e os pontos [tex]A,B,C[/tex] e [tex]D[/tex] tais que:
- o segmento [tex]\overline{AB}[/tex] tem [tex]6[/tex] cm de comprimento e está contido em [tex]\alpha [/tex];
- o segmento [tex]\overline{BC}[/tex] tem [tex]24[/tex] cm de comprimento, está contido em [tex]\alpha [/tex] e é perpendicular a [tex]\overline{AB}[/tex];
- o segmento [tex]\overline{AD}[/tex] tem [tex]8[/tex] cm de comprimento e é perpendicular a [tex]\alpha [/tex].
Nessas condições, calcule a medida do segmento [tex]\overline{CD}[/tex].
Extraído de EsPCEx.
Solução
De acordo com o enunciado, podemos construir a seguinte figura:
Aplicando o Teorema de Pitágoras no triângulo [tex]ABC[/tex], vem:
[tex]\qquad AC^2=AB^2+BC^2=6^2+24^2=612\text{ cm}^2.[/tex]
Agora, aplicando o Teorema de Pitágoras no triângulo [tex]ADC[/tex], temos:
[tex]\qquad CD^2=AD^2+AC^2=8^2+612=676\text{ cm}^2.[/tex]
Portanto,
[tex]\qquad CD=26\text{ cm}.[/tex]
Solução elaborada pelos Moderadores do Blog.
