✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 1º ano do E. M.)
Numa fazenda, havia [tex]20\%[/tex] de floresta. Para aumentar essa área, o dono da fazenda decidiu iniciar um processo de reflorestamento. No planejamento do reflorestamento, foi elaborado um gráfico fornecendo a previsão da porcentagem de área de floresta na fazenda a cada ano, num período de [tex]10[/tex] anos.
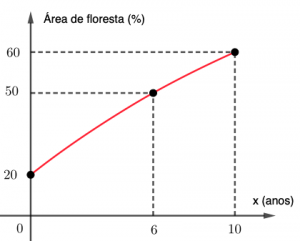
Esse gráfico foi modelado pela função [tex]f[/tex] definida por [tex]f(x)=\dfrac{ax+200}{bx+c}[/tex], que fornece a porcentagem de área na fazenda a cada ano [tex]x[/tex], sendo [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] constantes reais.
Com base nessas informações, reescreva a expressão que define a função [tex]f[/tex] com as constantes [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] determinadas.
Extraído de Vunesp-SP.
Solução
Vamos usar as informações fornecidas pelo gráfico e a lei da função [tex]f[/tex] para obter um sistema de equações nas incógnitas [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex].
Inicialmente, observe que:
- [tex]f(0)=\dfrac{a\cdot 0+200}{b\cdot 0+c}=\dfrac{200}{c}[/tex],
- [tex]f(6)=\dfrac{a\cdot 6+200}{b\cdot 6+c}=\dfrac{ 6a+200}{ 6b+c}[/tex],
- [tex]f(10)=\dfrac{a\cdot 10+200}{b\cdot 10+c}=\dfrac{ 10a+200}{ 10b+c}[/tex].
Mas sabemos que [tex]f(0)=20[/tex], [tex]f(6)=50[/tex] e [tex]f(10)=60[/tex]; logo obtemos o seguinte sistema:
[tex]\qquad \begin{cases}20=\dfrac{200}{c}\\
50=\dfrac{6a+200}{ 6b+c}\\
60=\dfrac{10a+200}{10b+c}~~~~
\end{cases}[/tex].
A primeira equação do sistema fornece [tex]c=10[/tex]. Substituindo esse valor nas outras equações, obtemos um novo sistema
[tex]\qquad\begin{cases}50=\dfrac{ 6a+200}{ 6b+10}\\
60=\dfrac{ 10a+200}{ 10b+10}~~\end{cases}[/tex]
e esse sistema é equivalente a
[tex]\qquad\begin{cases}300b+500= 6a+200\\
600b+600=10a+200~~
\end{cases}[/tex].
No último sistema, multiplicando a primeira equação por [tex]2[/tex] e subtraindo o resultado da segunda obtemos
[tex]\qquad -400=-2a-200\\
\qquad a=100.[/tex]
Finalmente, substituindo o valor de [tex]a[/tex] na equação [tex]600b+600=10a+200[/tex], segue que:
[tex]\qquad 600b+600=1000+200\\
\qquad b=1[/tex]
e, portanto, a função [tex]f[/tex] pode ser definida como [tex]~\fcolorbox{black}{#eee0e5}{$f(x)=\dfrac{100x+200}{x+10}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
