Problema
(Indicado a partir do 9º ano do E. F.)
Considere os quadrados dispostos como na figura:
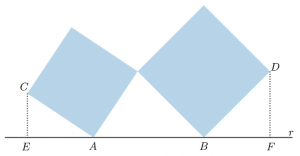
Sabendo-se que a distância do ponto [tex]C[/tex] à reta [tex]r[/tex] é de [tex]2[/tex] cm e que a distância do ponto [tex]D[/tex] à reta [tex]r[/tex] é de [tex]3[/tex] cm, calcule a medida do segmento [tex]\overline{AB}[/tex].
Solução
Seja [tex]H[/tex] o ponto comum aos quadrados, como na figura abaixo. Vamos traçar o segmento de reta [tex]\overline{HG}[/tex], perpendicular a [tex]r[/tex] passando por [tex]H[/tex].
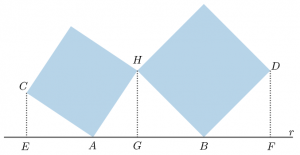
Os triângulos [tex]CEA[/tex] e [tex]AGH[/tex] são congruentes pelo caso A.L.A. (ângulo-lado-ângulo). De fato:
- [tex]CA=AH[/tex], por serem lados de um quadrado.
- Como os triângulos [tex]CEA[/tex] e [tex]AGH[/tex] são retângulos em [tex]E[/tex] e [tex]G[/tex], respectivamente, então
[tex]\qquad \angle CAE+\angle ECA=90^\circ[/tex]
[tex]\qquad\angle CAE+90^\circ+\angle HAG=180^\circ \ \ \therefore \ \ \angle CAE+\angle HAG=90^\circ.[/tex]Logo,
[tex]\qquad\angle ECA=\angle HAG.[/tex] -
Como a soma dos ângulos internos de um triângulo deve somar [tex]180^\circ [/tex], segue que
[tex]\qquad \angle EAC=\angle AHG.[/tex]
Assim, os triângulos [tex]CEA[/tex] e [tex]AGH[/tex] são congruentes, e [tex]CE=AG[/tex].
De forma totalmente análoga, prova-se que os triângulos [tex]GBH[/tex] e [tex]FDB[/tex] são congruentes e [tex]GB=FD[/tex]. Desta forma,
[tex]\qquad AB=AG+GB=CE+FD=2+3=5[/tex] cm.
Solução elaborada pelos Moderadores do Blog.
