✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.) (Nível: Médio)
(ENEM 2012 – adaptado) Durante seu treinamento, um atleta percorre metade de uma pista circular de raio [tex]r[/tex], conforme figura abaixo. A sua largada foi dada na posição representada pela letra [tex]L[/tex], a chegada está representada pela letra [tex]C[/tex] e a letra [tex]A[/tex] representa o próprio atleta.
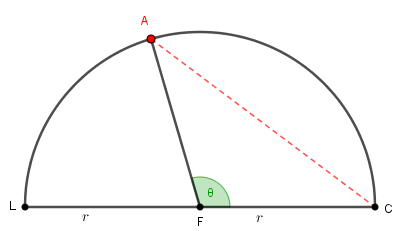
Se [tex]\theta[/tex] é a medida do ângulo que [tex]\overline{AF}[/tex] faz com [tex]\overline{FC}[/tex], qual o valor em graus de [tex]\theta[/tex], no momento da corrida em que o segmento [tex]\overline{AC}[/tex] medir [tex]r[/tex]?
Um aplicativo para ajudar
Você pode utilizar o applet abaixo para tentar visualizar o valor de [tex]\theta[/tex].
Movimente o ponto [tex]\textcolor{red}{A}[/tex] para obter segmentos [tex]\overline{AC}[/tex] com comprimentos próximos ao valor de [tex]r[/tex] e observe os respectivos valores de [tex]\theta[/tex] .
Instruções:
1) Aguarde o aplicativo carregar completamente.
2) Para movimentar o ponto [tex]\textcolor{red}{A}[/tex] sobre a semicircunferência, clique sobre ele, mantenha o mouse pressionado e faça o movimento.
3) Para reiniciar a movimentação, clique sobre as setinhas que aparecem no canto superior direito do aplicativo.
4) Lembre-se de que o GeoGebra fornece valores aproximados e que a visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
OBMEP_ srdg, criado com o GeoGebra
Solução
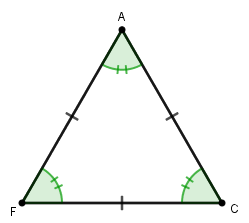
Note que o segmento [tex]\overline{AF}[/tex] é um raio da circunferência, assim, quando [tex]\overline{AC}[/tex] medir [tex]r[/tex], o triângulo [tex]FAC[/tex] será equilátero.
- Uma característica de triângulos equiláteros é que eles têm lados congruentes e ângulos internos congruentes, logo os três ângulos internos do triângulo [tex]FAC[/tex] têm medida [tex]\theta[/tex].
- Por outro lado, a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex], logo [tex]3\theta=180^\circ [/tex].
Dessa forma, temos que [tex]\, \theta=\dfrac{180^\circ}{3}[/tex], ou seja, [tex]\fcolorbox{black}{#eee0e5}{$\theta=60^\circ$} [/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
