.Problema para ajudar na escola: Área de um quadrilátero com pontas

Link do problema para dispositivos da Apple.

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)

(ONEM, 2004 – Adaptado) Na figura, vemos uma circunferência de centro em

$O$ que tangencia os lados

$\overline{AD}$ e

$\overline{BC}$ do retângulo

$ABCD$ nos pontos

$E$ e

$F$ , respectivamente.

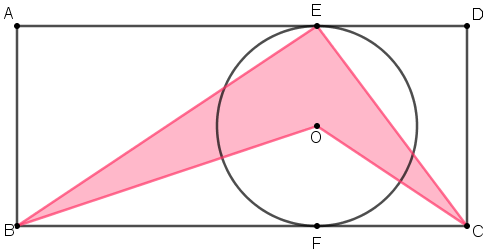
Se o retângulo $ABCD$ tem uma área de $40\, cm^2$ , qual é a medida da área do quadrilátero colorido $OCEB$ ?

Lembretes e notações

Uma reta tangente a uma circunferência é perpendicular ao raio no seu ponto de tangência.
Dado um ponto $P$ fora de uma dada reta $r$ , existe uma única reta perpendicular a $r$ passando por $P$ .
Para facilitar a notação, denotaremos o comprimento em centímetros do raio da circunferência da figura por $r$ e os comprimentos em centímetros dos lados $\overline{AE}$ e $\overline{ED}$ por $a$ e $b$ respectivamente.

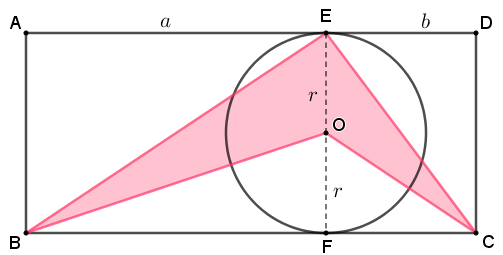
Solução 1

Observe, inicialmente, que os segmentos $\overline{AD}$ e $\overline{BC}$ são paralelos, já que eles são lados opostos de um retângulo. Dessa forma, utilizando os Lembretes (1) e (2), podemos concluir que:

os pontos $O$ , $E$ e $F$ são colineares;
a reta determinada por $O$ , $E$ e $F$ é perpendicular a $\overline{AD}$ e a $\overline{BC}$ ;
os segmentos $\overline{AB}$ e $\overline{DC}$ têm comprimento $2r$ .

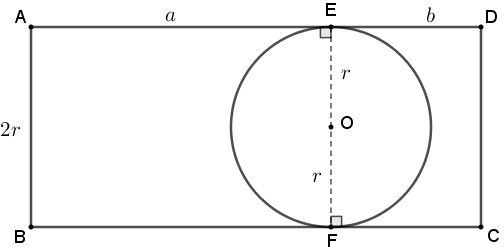
Por outro lado, observe que a área do retângulo $ABCD$ pode ser decomposta como a soma das áreas dos triângulos $ABE$ , $BCO$ e $CDE$ e do quadrilátero $OCEB$ . Portanto, calcularemos as medidas $A_1$ , $A_2$ e $A_3$ das respectivas áreas desses três triângulos para obtermos a área $\textcolor{#FF3366}{A}$ solicitada no problema.

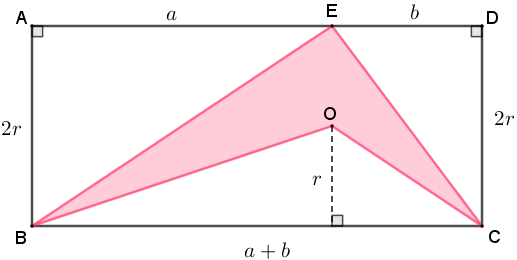
Vamos aos cálculos!

Triângulo $ABE$ :

$\;A_1=\dfrac{a \cdot 2r}{2}=a \cdot r$ .

Triângulo $BCO$ :

$\;A_2=\dfrac{(a+b) \cdot r}{2}$ .

Triângulo $CDE$ :

$\;A_3=\dfrac{b \cdot 2r}{2}=b \cdot r$ .

Como $\boxed{A_1+A_2+A_3+\textcolor{#FF3366}{A}=(a+b) \cdot 2r}$ , segue que:
$\qquad a \cdot r+\dfrac{(a+b) \cdot r}{2}+b \cdot r+\textcolor{#FF3366}{A}=(a+b) \cdot 2r$
$\qquad (a+b) \cdot r+\dfrac{(a+b) \cdot r}{2}+\textcolor{#FF3366}{A}=(a+b) \cdot 2r$
$\qquad 2 \cdot (a+b) \cdot r+(a+b) \cdot r+2 \cdot \textcolor{#FF3366}{A}=4 \cdot (a+b) \cdot r$
$\qquad 3 \cdot (a+b) \cdot r+2 \cdot \textcolor{#FF3366}{A}=4 \cdot (a+b) \cdot r$
$\qquad 2 \cdot \textcolor{#FF3366}{A}=4 \cdot (a+b) \cdot r-3 \cdot (a+b) \cdot r$
$\qquad 2 \cdot \textcolor{#FF3366}{A}= (a+b) \cdot r$
$\qquad \textcolor{#FF3366}{A}= \dfrac{(a+b) \cdot r}{2}. \qquad \qquad \textcolor{#800000}{(i)}$
Mas sabemos que o retângulo $ABCD$ tem uma área de $40\, cm^2$ ; assim:
$\qquad 40=(a+b)\cdot 2r$
$\qquad (a+b)\cdot r=20. \qquad \qquad \textcolor{#800000}{(ii)}$
Substituindo $\textcolor{#800000}{(ii)}$ em $\textcolor{#800000}{(i)}$ , obtemos:
$\qquad \textcolor{#FF3366}{A}= \dfrac{20}{2}=10$ .
Logo, a medida da área do quadrilátero colorido $\textcolor{#FF3366}{OCEB}$ é $\, \fcolorbox{black}{#eee0e5}{$10\, cm^2$}$ .

Solução elaborada pelos Moderadores do Blog.

Solução 2

os pontos $O$ , $E$ e $F$ são colineares;
a reta determinada por $O$ , $E$ e $F$ é perpendicular a $\overline{AD}$ e a $\overline{BC}$ ;
os segmentos $\overline{AB}$ e $\overline{DC}$ têm comprimento $2r$ .

Para esta solução, observe que a área do quadrilátero $OCEB$ pode ser decomposta como a soma das áreas dos triângulos $EBO$ e $EOC$ . Portanto, calcularemos as medidas $A_1$ e $A_2$ das áreas desses dois triângulos para obtermos a área $\textcolor{#FF3366}{A}$ solicitada no problema.

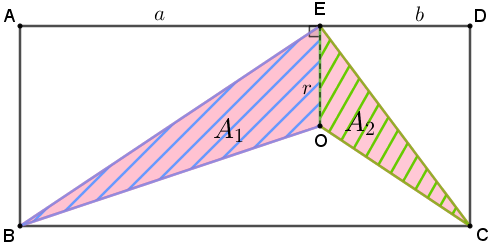
Em ambos os casos, utilizaremos o segmento $OE$ como base.

Triângulo $EBO$ :

$\quad A_1=\dfrac{a \cdot r}{2}$ .

Triângulo $EOC$ :

$\quad A_2=\dfrac{b \cdot r}{2}$ .

Como $\boxed{\textcolor{#FF3366}{A}=A_1+A_2}$ , segue que:
$\qquad\textcolor{#FF3366}{A}=\dfrac{a \cdot r}{2}+\dfrac{b \cdot r}{2}\\ \qquad \textcolor{#FF3366}{A}= \dfrac{(a+b) \cdot r}{2}. \qquad \qquad \textcolor{#800000}{(iii)}$
Mas sabemos que o retângulo $ABCD$ tem uma área de $40\, cm^2$ ; assim:
$\qquad 40=(a+b)\cdot 2r$
$\qquad (a+b)\cdot r=20. \qquad \qquad \textcolor{#800000}{(iv)}$
Substituindo $\textcolor{#800000}{(iv)}$ em $\textcolor{#800000}{(iii)}$ , obtemos:
$\qquad \textcolor{#FF3366}{A}= \dfrac{20}{2}=10$ .
Logo, a medida da área do quadrilátero colorido $\textcolor{#FF3366}{OCEB}$ é $\, \fcolorbox{black}{#eee0e5}{$10\, cm^2$}$ .

Solução elaborada pelos Moderadores do Blog.

Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo.
Você pode abrir o arquivo diretamente no seu navegador (Chrome, Edge, Firefox, Safari, entre outros), mas também pode utilizar o software gratuito Adobe Acrobat Reader.
Caso o dispositivo que você está utilizando não tenha o Acrobat Reader instalado, é só clicar AQUI para fazer o download adequado ao seu dispositivo.

Arquivo