.Problema Olímpico – Nível C: Quantas retas? – Clubes de Matemática da OBMEP

Problema

Considere dez pontos dispostos como na figura abaixo. Por cada dois pontos distintos é traçada uma reta.
Quantas retas distintas foram traçadas?

Solução

Para cada um dos

$10$ pontos, teremos outros

$9$ pontos para fazermos “par” com este primeiro e traçarmos uma reta sobre eles. Assim, a princípio, temos

$10\cdot9 = 90$ pares.
Mas, nesse caso, estamos contando uma mesma reta duas vezes: a reta que passa por um ponto, digamos

$A$ , e por outro ponto, digamos

$B$ , é a mesma que passa pelo ponto

$B$ e pelo ponto

$A$ . Logo foram traçadas, a princípio,

$\dfrac{90}{2} = 45$ retas.
No entanto, ainda estamos contando retas repetidas, veja:

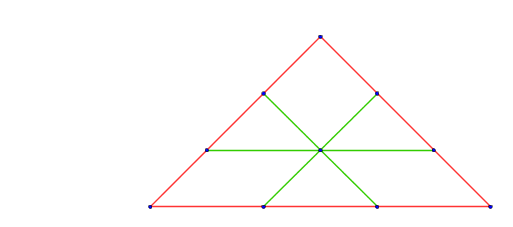
Atividade 1

As retas vermelhas e verdes se repetem, pois passam por mais de dois pontos na figura.

As retas vermelhas passam por $4$ pontos e há $C^2_4 = \dfrac{4!}{2!(4 -2)!} = \dfrac{12}{2} = 6$ maneiras de escolhermos $2$ pontos dentre esses $4$ . Assim, contamos cada reta vermelha $6$ vezes; como queremos contar apenas retas distintas, dentre as retas vermelhas temos $3\cdot(6 -1) = 15$ retas que precisamos “excluir”.
Utilizando o mesmo raciocínio com relação às retas verdes, vemos que elas passam por $3$ pontos e há $C^2_3 = \dfrac{3!}{2!(3 – 2)!} = 3$ maneiras de escolhermos $2$ pontos dentre $3$ . Assim, temos que “excluir” $\,3\cdot(3-1) = 6$ retas verdes.

Portanto, foram traçadas exatamente $\boxed{\,45-15-6 = 24\,}$ retas distintas.

Solução elaborada pelas alunas do PIC-OBMEP Andressa Wickert Kreutz e Noemi Zeraick Monteiro.