.Problema: O Mapa

Problema
(Indicado a partir do 8º ano do E. F.)

O mapa abaixo mostra uma estrada retilínea que passa sucessivamente pelas cidades

$A$ ,

$B$ e

$C$ .

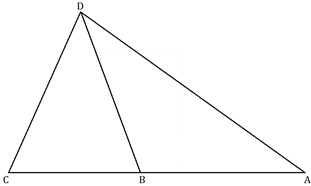
Outra cidade,

$D$ , distante

$120 \, km$ de

$A$ , localiza-se de tal forma que o

$\angle{DAB}=36^\circ$ .
Um viajante fez o trajeto de

$A$ para

$B$ , de

$B$ para

$D$ e de

$D$ para

$C$ , onde

$AB=BD=DC$ .
Se o viajante tivesse ido diretamente de

$A$ até

$C$ , qual a distância que ele teria percorrido?

Solução

Observe os ângulos mostrados na figura abaixo.

Como $AB=BD$ , o triângulo $ABD$ é isósceles e como $\angle{DAB}=36^\circ$ , então $\angle{BDA}=36^\circ$ .
Como a soma dos ângulos internos do triângulo $ABD$ é $180^{\circ}$ , então $\angle{ABD}=180^\circ -36^\circ -36^\circ=108^\circ$ .
Como os ângulos $A\hat{B}D$ e $D\hat{B}C$ são suplementares, então $\angle{DBC}=180^\circ-108^\circ=72^\circ$ .
Como $BD=DC$ , o triângulo $BCD$ é isósceles; assim, $\angle{DCB}=\angle{DBC}=72^\circ$ .
A soma dos ângulos internos do triângulo $BCD$ é $180^{\circ}$ , então $\angle{CDB}=180^\circ -72^\circ -72^\circ=36^\circ$ .

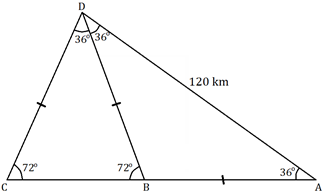
Veja que o triângulo $ACD$ é isósceles, com os ângulos da base $\overline{DC}$ medindo $72^\circ$ ; portanto, se o viajante tivesse ido diretamente de $A$ até $C$ , teria percorrido uma distância $\boxed{AC=AD=120 \, km} \, .$

Solução elaborada pelos Moderadores do Blog.