Problema
(Indicado a partir do 9º ano do E. F.)
(UFRJ, 2008) Uma prateleira de um metro de comprimento e [tex]4,4 \;cm[/tex] de espessura deve ser encaixada entre duas paredes planas e paralelas. Por razões operacionais, a prateleira deve ser colocada enviesada (inclinada), para depois ser girada até a posição final, como indica a figura.
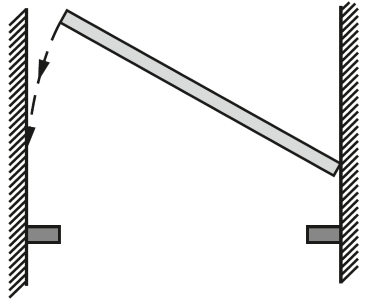
Se a distância entre as paredes é de um metro e um milímetro, é possível encaixar a prateleira?
Solução
Observe que, para que a prateleira seja encaixada, é necessário e suficiente que a diagonal do retângulo cujos lados são a espessura e o comprimento da prateleira seja menor do que a distância entre as paredes. A diagonal em questão é a hipotenusa do triângulo retângulo destacado na figura abaixo.
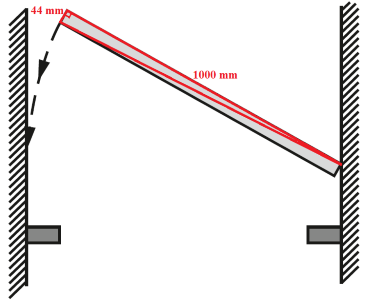
Sendo [tex]d[/tex] a diagonal, aplicando o teorema de Pitágoras ao triângulo, temos
[tex]\qquad d = \sqrt{44^2+1\;000^2} = \sqrt {1\;001\;936} \;mm.[/tex]
Agora, repare que um metro e um milímetro correspondem a [tex]1\;001 \;mm[/tex], e além disso, [tex]1\;001^2 = 1\;002\;001.[/tex] Portanto,
[tex]\qquad d = \sqrt {1\;001\;936} \;mm\lt\sqrt{1\;002\;001}\;mm= 1\;001 \;mm[/tex], ou seja,
[tex]\qquad d\lt 1\;001 \;mm.[/tex]
Logo, é possível encaixar a prateleira.
Solução elaborada pelos Moderadores do Blog.
