Problema
(Indicado a partir do 2º ano do E. M.)
Um bloco de madeira, com a forma de um prisma reto retangular, foi serrado na parte superior e deu origem ao sólido da figura abaixo
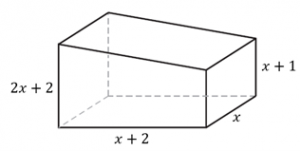
Com base nas informações da figura, qual o volume desse sólido?
Adaptado de Unimontes.
Solução
Observando de lado, o sólido em questão é um prisma cuja base é um trapézio. Dessa forma, o volume é dado pelo produto da área da base pela altura do prisma.
A área da base [tex](A_b)[/tex], corresponde à área de um trapézio de bases medindo [tex]2x+2[/tex] e [tex]x+1[/tex] e altura [tex]x+2[/tex]. Assim, temos:
[tex]\qquad A_b=\dfrac{(2x+2+x+1)\cdot (x+2)}{2}=\dfrac{3\cdot (x+1)\cdot (x+2)}{2}.[/tex]
A altura do prisma corresponde à distância entre as bases, portanto, [tex]x[/tex].
Finalmente, o volume do prisma é dado por:
[tex]\qquad V=\dfrac{3(x+1)(x+2)}{2}\cdot x=\dfrac{3x(x+1)(x+2)}{2}.[/tex]
Solução elaborada pelos Moderadores do Blog.
