.Problema: Distância na casa

Problema
(Indicado a partir do 2º ano do E. M.)

(UFPE-2002) O formato de uma casa é

• o de um prisma reto de altura $12\ m$, tendo por base um triângulo isósceles de base $8\ m$ e altura $3\ m$,
• e o de um paralelepípedo reto retângulo de dimensões $8\ m$, $12\ m$ e $3\ m$.

A face retangular de dimensões $8\ m$ e $12\ m$ do prisma coincide com uma face do paralelepípedo conforme mostra figura abaixo.

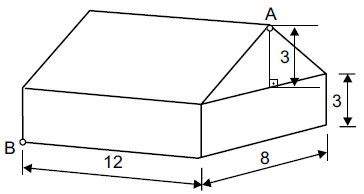
Qual a distância, em metros, entre os pontos $A$ e $B$?

Solução

Observe a figura abaixo.

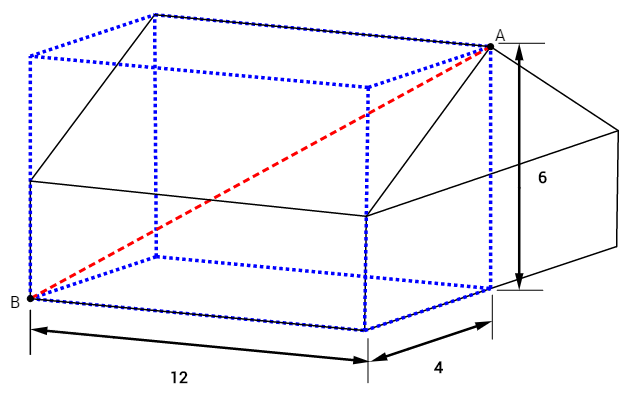
Sabemos que a expressão $d=\sqrt{a^2+b^2+c^2}$ corresponde à diagonal de um paralelepípedo de dimensões $a$, $b$ e $c$.
Na figura do problema, vemos um paralelepípedo cujas dimensões são $a=12$, $b=3+3=6$ e $c=8:2=4$ e cuja diagonal corresponde à distância entre os pontos $A$ e $B$ solicitada.
Assim, essa distância é dada por $d=\sqrt{12^2+6^2+4^2}=14$ metros.

Solução elaborada pelos Moderadores do Blog.