Problema
(Indicado a partir do 2º ano do E. M.)
Uma esfera de 2 cm de raio é colocada no interior de um vaso cônico, conforme a figura a seguir. O vaso tem 12 cm de altura e sua abertura é uma circunferência com 5 cm de raio. Nessas condições, calcule a menor distância ([tex]d[/tex]) entre a esfera e o vértice do cone.
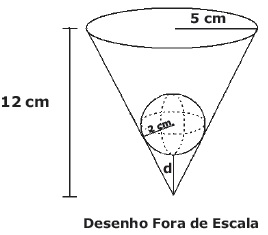
Extraído de EsPCEx.

AJUDAS
(I) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(II) Em triângulos semelhantes, os lados correspondentes são proporcionais.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
(III) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução
De acordo com os dados no enunciado e utilizando o Teorema de Pitágoras, podemos destacar dois triângulos retângulos e algumas de suas medidas:
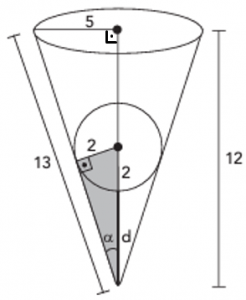
Observe que os dois triângulos são semelhantes pelo caso de Semelhança A.A. Assim, podemos montar a seguinte proporção:
[tex]\qquad \dfrac{2}{d+2}=\dfrac{5}{13},[/tex]
[tex]\qquad 5d+10=26,[/tex]
[tex]\qquad d=\dfrac{16}{5}={3,2 \text{ cm}}.[/tex]
Solução elaborada pelos Moderadores do Blog.
