✏ Link do problema para dispositivos da Apple.
Problema
Na figura abaixo vemos um triângulo equilátero [tex]ABC[/tex] cuja circunferência a ele inscrita é tangenciada pela reta que passa pelos pontos [tex]M[/tex] e [tex]N[/tex], pontos estes pertencentes a lados do triângulo.
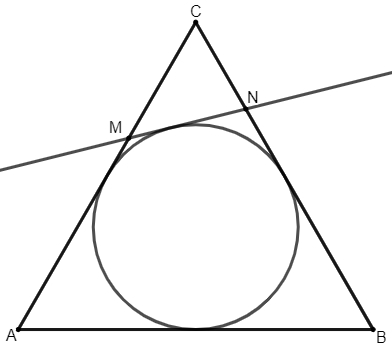
Determine o valor de [tex]\boxed{\dfrac{CM}{MA}+\dfrac{CN}{NB}}\,.[/tex]
Notações e Lembretes
✏ Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
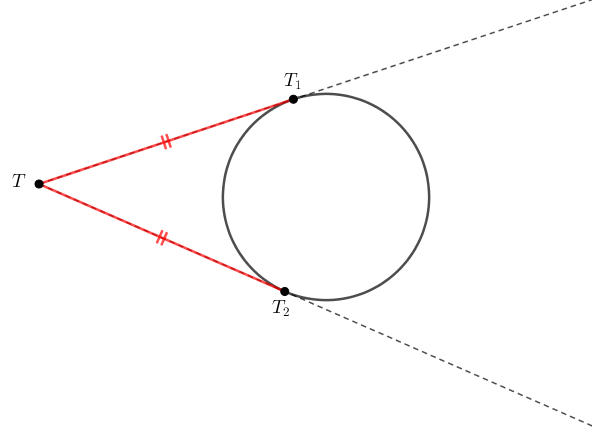
(I) (Relação dos segmentos tangentes) Se de um ponto [tex]T[/tex] conduzirmos os segmentos [tex]\overline{TT_1}[/tex] e [tex]\overline{TT_2}[/tex] tangentes a uma circunferência, sendo [tex]T_1[/tex] e [tex]T_2[/tex] pontos da circunferência, então [tex]\overline{TT_1}[/tex] e [tex]\overline{TT_2}[/tex] têm o mesmo comprimento.
(II) (Lei dos Cossenos) Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] valem as relações:
[tex]\qquad {\displaystyle a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot cos{\widehat {A}}\,\!}[/tex];
[tex]\qquad {\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot cos{\widehat {B}}\,\!}[/tex];
[tex]\qquad {\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot cos{\widehat {C}}\,\!}[/tex].
Solução
Vamos observar, inicialmente, apenas o triângulo equilátero [tex]ABC[/tex] e a circunferência a ele inscrita.
Aplicando o Lembrete I sucessivamente
- ao vértice [tex]A[/tex] e aos pontos de tangência [tex]T_1[/tex] e [tex]T_2[/tex];
- ao vértice [tex]B[/tex] e aos pontos de tangência [tex]T_2[/tex] e [tex]T_3[/tex];
- ao vértice [tex]C[/tex] e aos pontos de tangência [tex]T_1[/tex] e [tex]T_3[/tex];
concluímos que [tex]AT_1=AT_2[/tex], [tex]BT_2=BT_3[/tex] e [tex]CT_1=CT_3[/tex]. Indicaremos esses comprimentos por [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex], respectivamente, de acordo com a figura a seguir.
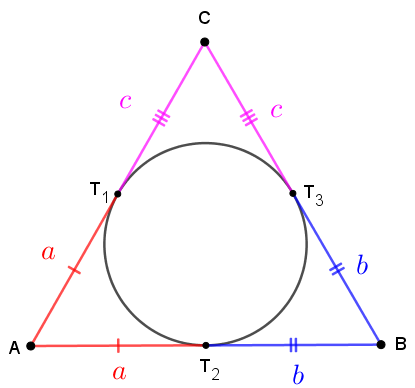
Como o triângulo [tex]ABC[/tex] é equilátero, segue que [tex]a+b=b+c=a+c[/tex] e, portanto, [tex]a=b=c.[/tex] Podemos então simplificar a imagem do triângulo [tex]ABC.[/tex]
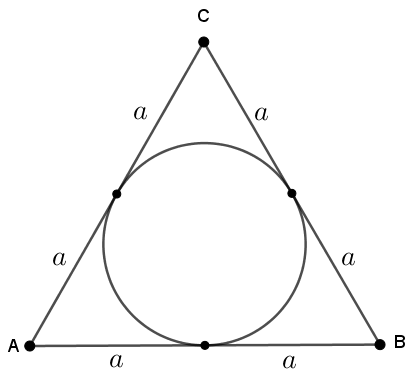
Vamos observar agora o triângulo [tex]ABC[/tex], a circunferência a ele inscrita, a reta tangente que passa pelos pontos [tex]M[/tex] e [tex]N[/tex] e o ponto de tangência [tex]T_4.[/tex]
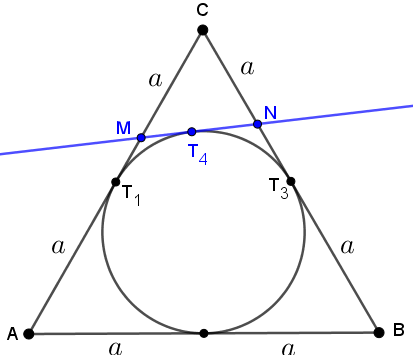
Podemos aplicar o Lembrete I, também,
- ao ponto [tex]M[/tex] e aos pontos de tangência [tex]T_1[/tex] e [tex]T_4[/tex];
- ao ponto [tex]N[/tex] e aos pontos de tangência [tex]T_3[/tex] e [tex]T_4[/tex];
e concluir que [tex]MT_1=MT_4[/tex] e [tex]NT_3=NT_4[/tex]. Indicaremos esses comprimentos por [tex]x[/tex] e [tex]y[/tex], respectivamente, de acordo com a figura a seguir. Perceba que destacamos os comprimentos dos segmentos [tex]\overline{CM}[/tex] e [tex]\overline{CN}[/tex], para ajudar nos cálculos que faremos a seguir.
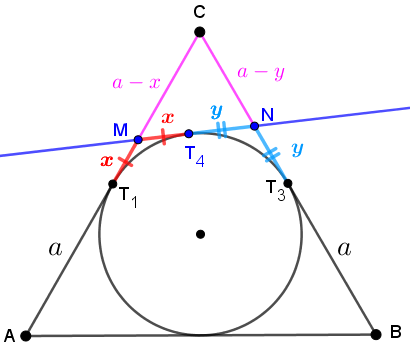
Vamos focar nossa atenção nos triângulos [tex]ABC[/tex] e [tex]MNC[/tex] com as medidas que já conhecemos, acrescidas da medida do ângulo de vértice [tex]C[/tex] que sabemos ser [tex]60^\circ[/tex], já que o triângulo [tex]ABC[/tex] é equilátero.
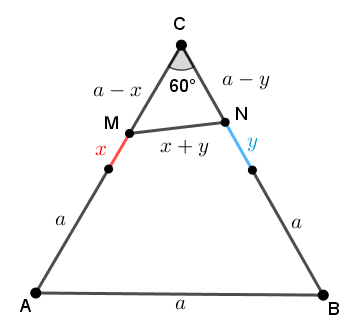
Vamos calcular, então o valor de [tex]\boxed{\dfrac{CM}{MA}+\dfrac{CN}{NB}}:[/tex]
[tex]\qquad \dfrac{CM}{MA}+\dfrac{CN}{NB}=\dfrac{a-x}{a+x}+\dfrac{a-y}{a+y}\\
\qquad \dfrac{CM}{MA}+\dfrac{CN}{NB}=\dfrac{(a-x)\cdot (a+y)+(a-y)\cdot (a+x)}{(a+x)\cdot (a+y)}\\
\qquad \dfrac{CM}{MA}+\dfrac{CN}{NB}=\dfrac{a^2+ay-ax-xy+a^2+ax-ay-xy}{(a+x)\cdot (a+y)}\\
\qquad \dfrac{CM}{MA}+\dfrac{CN}{NB}=\dfrac{a^2-xy+a^2-xy}{(a+x)\cdot (a+y)}\\
\qquad \dfrac{CM}{MA}+\dfrac{CN}{NB}=\dfrac{2a^2-2xy}{(a+x)\cdot (a+y)}.\qquad \textcolor{#800000}{(i)}\\
[/tex]
Agora, vamos aplicar a Lei dos cossenos (Lembrete II), ao vértice [tex]C[/tex] do triângulo [tex]MNC[/tex]
[tex] \qquad \left(x+y\right)^2=\left(a-x\right)^2+\left(a-y\right)^2-2\cdot \left(a-x\right)\cdot \left(a-y\right) \cdot cos60^\circ\\
\qquad \left(x+y\right)^2=\left(a-x\right)^2+\left(a-y\right)^2-2\cdot \left(a-x\right)\cdot \left(a-y\right) \cdot \dfrac{1}{2}\\
\qquad \left(x+y\right)^2=\left(a-x\right)^2+\left(a-y\right)^2-\left(a-x\right)\cdot \left(a-y\right) \\
\qquad x^2+2xy+y^2=a^2-2ax+x^2+a^2-2ay+y^2-\left(a^2-ay-ax+xy\right)\\
\qquad x^2+2xy+y^2=a^2-2ax+x^2+a^2-2ay+y^2-a^2+ay+ax-xy\\
\qquad x^2+2xy+y^2=2a^2-ax+x^2-ay+y^2-a^2-xy\\
\qquad\cancel{x^2}+2xy+\bcancel{y^2}=2a^2-ax+\cancel{x^2}-ay+\bcancel{y^2}-a^2-xy\\
\qquad 0=2a^2-ax-ay-a^2-xy-2xy\\
\qquad 2a^2-2xy=ax+ay+a^2+xy\\
\qquad 2a^2-2xy=(a^2+ax)+(ay+xy)\\
\qquad 2a^2-2xy=a\cdot \left(a+x\right)+y\cdot \left(a+x\right)\\
\qquad2a^2-2xy=\left(a+x\right)\cdot \left(a+y\right)\\
\qquad \dfrac{2a^2-2xy}{\left(a+x\right)\cdot \left(a+y\right)}=1.\qquad \textcolor{#800000}{(ii)}\\
[/tex]
Portanto, por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], segue que [tex]\fcolorbox{black}{#FFEEEF}{$\dfrac{CM}{MA}+\dfrac{CN}{NB}=1$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível B – Questão Difícil
