Problema
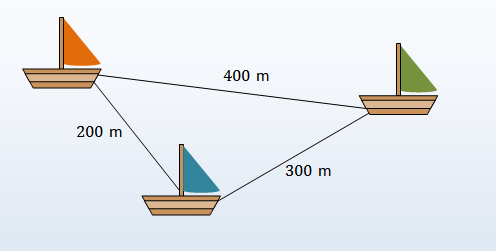
Três navios A, B e C estão dispostos no mar de tal modo que a distância entre A e B é [tex]300[/tex] m, a distância entre A e C é [tex]200[/tex] m e a distância entre B e C é [tex]400[/tex] m.
Quanto aos ângulos formados pelos lados do triângulo determinado por esses navios podemos afirmar que:
(a) um deles é reto.
(b) um deles é obtuso.
(c) todos são iguais.
(d) dois são obtusos.
(e) nenhuma das alternativas anteriores.
Solução
Considere o triângulo definido pelos três navios.
 |
➞ |
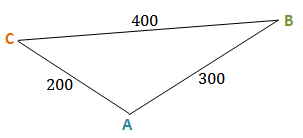 |
Observe que [tex]400^2 > 200^2 + 300^2[/tex]; deste modo, um dos ângulos é obtuso.
Solução elaborada pelos Moderadores do Blog.
Um aplicativo para ajudar…
Aguardem o aplicativo carregar completamente.
Lembrem-se de que, se em um triângulo cujos lados medem [tex]a, \, b \, [/tex] e [tex] \, c \, [/tex] tivermos [tex]a^2=b^2+c^2[/tex], então esse triângulo é retângulo e, portanto, tem um ângulo reto.
No applet abaixo, temos um triângulo [tex]ABC[/tex] inicial que mostra aproximadamente a situação dos navios descritos no enunciado do problema.
Movimentem o ponto [tex]C[/tex] e percebam a relação entre o lado de comprimento [tex]a \, [/tex] e o seu ângulo oposto.
Ao movimentar o ponto [tex]C[/tex], apenas a medida do lado [tex]\overline{BC}[/tex] é modificada: as medidas dos outros dois lados do triângulo permanecem as mesmas. Assim, em cada movimento, percebam também a relação entre [tex]a^2 \, [/tex] e [tex] \, b^2+c^2=130000[/tex].
OBMEP_ srdg, criado com o GeoGebra
Observações:
1) Para movimentar o ponto [tex]C[/tex], basta clicar sobre ele com o mouse e, mantendo o mouse pressionado, movimentá-lo.
2) Para voltar aos valores inicialmente definidos, cliquem nas setinhas que aparecem no canto superior direito do applet.
3) Lembrem-se de que o GeoGebra fornece valores aproximados para as medidas apresentadas.
Nível A – Questão Difícil
