✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir da 1ª série do E. M.)
Uma peça circular de centro [tex]C[/tex] e raio [tex]12[/tex] cm está suspensa por uma corda alaranjada, perfeitamente esticada e fixada em [tex]P[/tex]. Os pontos [tex]T[/tex] e [tex]Q[/tex] são de tangência dos segmentos retilíneos da corda com a peça, e a medida do ângulo agudo [tex]T\hat{P}Q[/tex] é [tex]60^\circ[/tex].
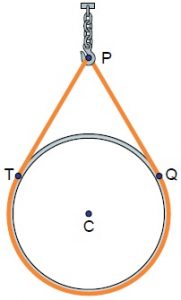
Calcule o comprimento aproximado da corda alaranjada.
Adote [tex]\pi=3,1[/tex], [tex]\sqrt{3}=1,7[/tex], despreze a espessura da corda, da peça circular e do gancho que a sustenta.
Extraído de VUNESP.
Lembretes e notações
(1) Para solucionar este problema, vamos precisar de uma das relações entre as medidas dos lados e dos ângulos internos de um triângulo retângulo. Vale a pena recordar essas relações!
Seja, então, um triângulo retângulo [tex]ABC[/tex], cujos lados têm comprimentos [tex]a,\, b,\, c\, [/tex] e os ângulos agudos têm medidas [tex]\alpha[/tex] e [tex]\beta[/tex], conforme indicado na figura.
Então: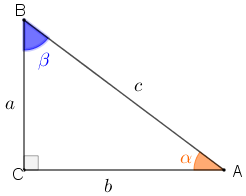
[tex]\bullet \, sen\, \hat{A}=sen\, \alpha=\dfrac{a}{c}=cos\, \beta=cos\, \hat{B}[/tex]
[tex]\bullet \, cos\, \hat{A}=cos\, \alpha=\dfrac{b}{c}=sen\, \beta=sen\, \hat{B}[/tex]
[tex]\bullet \, tan\, \hat{A}=tan\, \alpha=\dfrac{a}{b}[/tex]
[tex]\bullet \, tan\, \hat{B}=tan\, \beta=\dfrac{b}{a}[/tex]
(2) O comprimento [tex]c[/tex] do arco de uma circunferência de raio [tex]r[/tex] correspondente a um ângulo central cuja medida em graus é [tex]\alpha[/tex] é dado por [tex]~c=\dfrac{\alpha}{360^\circ}\cdot 2\pi r.[/tex]
(3) Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
(4) Relação dos segmentos tangentes: Se de um ponto [tex]T[/tex] conduzirmos os segmentos [tex]\overline{TT_1}[/tex] e [tex]\overline{TT_2}[/tex] tangentes a uma circunferência, sendo [tex]T_1[/tex] e [tex]T_2[/tex] pontos da circunferência, então [tex]\overline{TT_1}[/tex] e [tex]\overline{TT_2}[/tex] têm o mesmo comprimento.
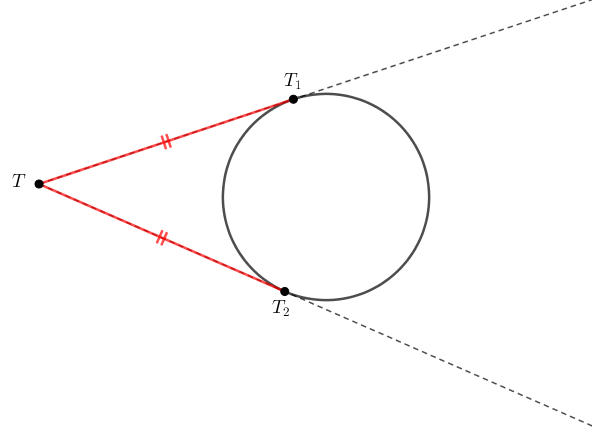(5) Congruência de triângulos retângulos: Se dois triângulos retângulos têm ordenadamente congruentes um cateto e a hipotenusa, então estes triângulos são congruentes.
(6) (Lei dos Senos) Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] vale a relação:
[tex]\qquad \dfrac{a}{sen \;\hat{A}} = \dfrac{b}{sen \;\hat{B}} = \dfrac{c}{sen \;\hat{C}} = 2R[/tex],
sendo [tex]R[/tex] o raio da circunferência circunscrita ao triângulo [tex]ABC[/tex].
(7) A soma das medidas dos ângulos internos de qualquer triângulo vale [tex]180^\circ[/tex].
✐ Notações:
– Denotaremos o ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]\angle{XVY} [/tex] e sua medida por [tex]X\hat{V}Y.[/tex]
– Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução 1
Sendo [tex]\overline{PQ}[/tex] e [tex]\overline{PT}[/tex] tangentes à circunferência, pelo Lembrete (3), temos [tex]P\hat{T}C = C\hat{Q}P = 90 ^\circ[/tex].
Como os triângulos [tex]PCQ[/tex] e [tex]PCT[/tex] são retângulos com [tex]CT=CQ[/tex], eles são congruentes, de acordo com o Lembrete (5). Consequentemente, os ângulos [tex]\angle{QPC} [/tex] e [tex]\angle{CPT} [/tex] têm a mesma medida; e, como [tex]T\hat{P}Q=60^\circ[/tex], segue que:
[tex]\quad Q\hat{P}C = C\hat{P}T = \dfrac {60^\circ}{2}=30^\circ[/tex]
e
[tex]\quad Q\hat{C}P= P\hat{C}T=90^\circ-30^\circ=60^\circ[/tex].
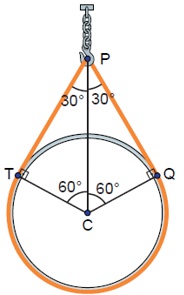
Agora, note que, no triângulo [tex]CPQ[/tex]:
[tex]\quad tan\; 30^\circ=\dfrac{QC}{PQ}\\
\quad \dfrac{\sqrt{3}}{3}=\dfrac{12}{PQ}\\
\quad PQ=\dfrac{36}{\sqrt{3}} \\
\quad PQ=\dfrac{36\times \sqrt{3}}{3} \\
\quad PQ=12 \times 1,7\\
\quad \boxed{PQ=20,4\text{ cm}}.[/tex]
Note, também, que o comprimento do arco de circunferência alaranjado, determinado pelos pontos [tex]Q~[/tex] e [tex]~T[/tex], corresponde a um ângulo central de [tex]360^\circ-2\cdot 60^\circ=240^\circ[/tex] e raio [tex]12 \text{ cm}.[/tex] Portanto, pelo Lembrete (2), o seu comprimento [tex]comp[/tex] é dado por:
[tex]\quad comp=\dfrac{240^\circ}{360^\circ}\times 2\pi \times 12\\
\quad comp=\dfrac{2}{3}\times 6.2 \times 12\\
\quad \boxed{comp=49,6\text{ cm}}.[/tex]
Finalmente, perceba que o comprimento da corda é igual à soma dos comprimentos de [tex]\overline{PT}[/tex], [tex]\overline{PQ}[/tex] e do arco de circunferência determinado pelos pontos [tex]Q~[/tex] e [tex]~T.[/tex] Logo, o comprimento [tex]C[/tex] da corda alaranjada é:
[tex]\quad C=20,4+20,4+49,6\\
\quad \textcolor{#800000}{\boxed{C=90,4 \text{ cm}}}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Primeiramente, traçando os segmentos [tex]\overline {CT}[/tex] e [tex]\overline {CQ}[/tex], que são raios da circunferência de centro [tex]C[/tex], temos que eles definem ângulos de [tex]90^\circ[/tex] no quadrilátero [tex]PQCT[/tex].
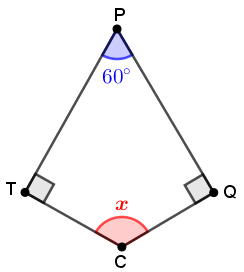Sendo assim, olhando para o quadrilátero [tex]PQCT[/tex], conhecemos três de seus ângulos internos. Logo, podemos fazer:[tex]\qquad 90^\circ+90^\circ+60^\circ +x=360^\circ\\
\qquad x=120^\circ.\\
~~[/tex]
Assim, o ângulo central [tex]T\hat CQ[/tex] vale [tex]120^\circ[/tex] e podemos assumir que o setor circular equivalente a ele também vale [tex]120^\circ[/tex], ou seja, um terço do comprimento [tex]c[/tex] da circunferência. Portanto, o valor que queremos encontrar corresponde ao que sobra da circunferência, ou seja, dois terços de [tex]c.[/tex]
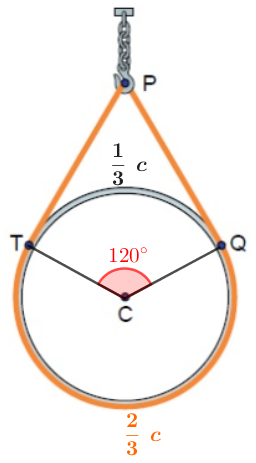Então, vamos encontrar esses valores:[tex]\quad c= 2 \pi r\\
\quad c=2 \times 3,1 \times 12\\
\quad c=74,4 \text{ cm}\\
\quad \dfrac{2}{3}~c=\dfrac{2\times 74,4}{3}\\
\quad \dfrac{2}{3}~c= 49,6 \text{ cm.}[/tex]
Agora, devemos encontrar o comprimento do resto da corda. Para isso, percebamos, a partir do Lembrete (4), que os segmentos [tex]\overline {TP}[/tex] e [tex]\overline {QP}[/tex] são congruentes e, com isso, temos que o triângulo [tex]PTQ[/tex] é isósceles.
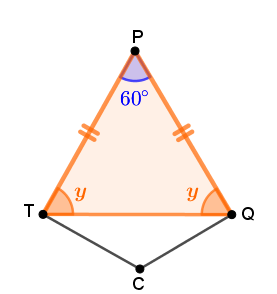
Considerando o Lembrete (7) e os ângulos internos desse triângulo temos que:
[tex]\quad 60^\circ+2y=180^\circ\\
\quad y=60^\circ.[/tex]
Logo, o triângulo [tex]PTQ[/tex] é equilátero.
Olhando agora para o triângulo [tex]CTQ[/tex], que também é isósceles, conseguimos descobrir a medida [tex]x[/tex] dos seus ângulos internos congruentes da seguinte forma:
[tex]\quad 120^\circ+2z=180^\circ\\
\quad z=30^\circ.[/tex]
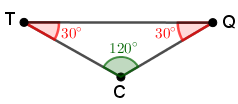
Utilizando a lei dos senos nesse triângulo, temos que:
[tex]\quad \dfrac{TQ}{sen\ 120^\circ}=\dfrac{12}{sen\ 30^\circ}\\
\quad \dfrac{TQ}{\frac{\sqrt 3}{2}}= \dfrac{12}{\frac{1}{2}}\\
\quad \dfrac{TQ}{\frac{1,7}{2}}= 24\\
\quad \dfrac{TQ}{0,85}= 24\\
\quad TQ= 24 \times 0,85\\
\quad TQ=20,4 \text{ cm.}[/tex]
Logo, [tex]{PQ}={PT}=20,4 \text{ cm}~[/tex] e, portanto, o comprimento da corda alaranjada pode ser assim calculado:
[tex]\quad \text{comprimento}=2 \times 20,4 + 49,6= \boxed{90,4 \text{ cm}}.[/tex]
Solução elaborada pelo COM Phidias, com contribuições dos Moderadores do Blog.