.Problema: Área do círculo

Problema
(Indicado a partir do 1º ano do E. M.)

Na figura, temos um círculo de diâmetro

$\overline{AB}$ que tangencia no ponto

$T$ a reta

$s$ que contém o diâmetro do semicírculo de centro

$O$ . Sendo

$\overline{AB}$ também uma corda do semicírculo,

$C$ a interseção de

$s$ com a reta

$\overleftrightarrow{AB}$ ,

$OT = 2\, cm$ e

$TC = 32\,cm$ , calcule a área do círculo.

Problema

Um convite
Aprendam um pouco sobre mediatriz nesta sala do Blog.

Solução

Seja

$D$ o centro do círculo e

$r$ seu raio.

A mediatriz de $\overline{AB}$ passa em $O$ , já que $O$ equidista de $A$ e $B$ . Além disso o raio $\overline{DT}$ do círculo é perpendicular à reta tangente.

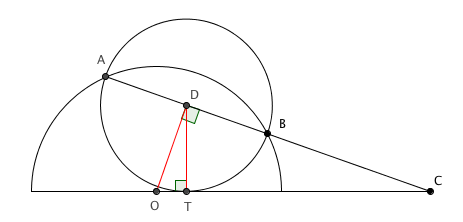
fig001

No triângulo retângulo $ODC$ , usaremos a SEGUINTE relação métrica:

o quadrado da altura relativa à hipotenusa é igual ao produto das projeções ortogonais dos catetos sobre a hipotenusa.

Assim,
$\qquad DT^2 = OT \cdot TC$
$\qquad r^2 = 2 \cdot 32$
$\qquad r^2 = 64$
e, portanto:
$\qquad \boxed{\textbf{Área do círculo} = \pi r^2 = 64 \pi\,cm^2}$ .

Solução elaborada pelos Moderadores do Blog.