.Problema: Área da Malha
Problema
(Indicado a partir do 8º ano do E. F.)
Em uma malha quadriculada [tex]1\times 1[/tex] foram construídas as figuras [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] abaixo.
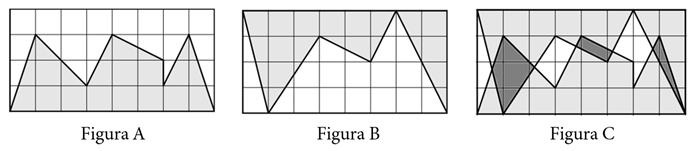
Calcule a área branca da figura [tex]C[/tex], sabendo que a área mais escura de [tex]C[/tex] vale [tex]4[/tex].
Solução 1
Adotando [tex]u[/tex] como unidade de medida, primeiramente, podemos visualizar que as áreas das figuras [tex]A[/tex] e [tex]B[/tex], podem ser divididas em um conjunto de triângulos e quadrados, da seguinte maneira:
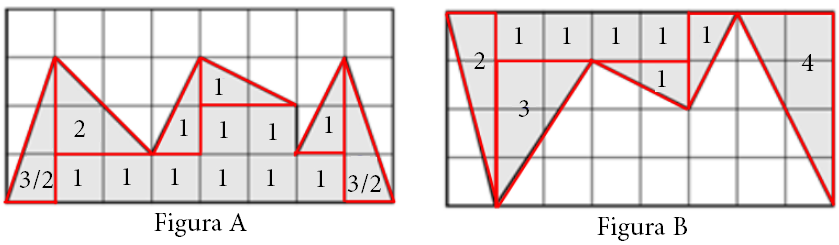
Como as figuras representam uma malha quadriculada com quadrados de lado igual a [tex]1\ u[/tex], não é difícil notar que a área de cada quadradinho é igual a [tex]1 \ u^2[/tex], e a área de cada triângulo pode ser calculada utilizando [tex]\frac{b \cdot h}{2}[/tex] (estas que já estão marcadas no interior de cada triângulo acima). Portanto, podemos descobrir a área cinza das figuras [tex]A[/tex] e [tex]B[/tex] apenas somando a área destes quadradinhos e triângulos:
[tex]\qquad A_A = 8 \cdot 1 + \frac{3}{2} + 2 + 1 + 1 + 1 + \frac{3}{2} = 16 \ u^2 \\[/tex]
[tex]\qquad
A_B = 4 \cdot 1 + 2 + 3 + 1 + 1 + 4 = 15 \ u^2[/tex]
Também não é difícil perceber que a figura [tex]C[/tex] é apenas uma união da figura [tex]A[/tex] com a figura [tex]B[/tex], enquanto a área mais escura representa as áreas sobrepostas destas figuras. Portanto, para descobrir a área em branco da figura [tex]C[/tex], basta calcularmos a área de toda a malha: [tex]8 \cdot 4 = 32 \ u^2[/tex]; calcularmos a área total ocupada pela união das figuras [tex]A[/tex] e [tex]B[/tex]: [tex]16 + 15 = 31 \ u^2[/tex] ; e desconsiderar a área mais escura de [tex]C[/tex] da soma anterior (pois caso contrário, estaríamos contando sua área duas vezes, por ser a interseção):
$$
A_{branca} = 32-(31-4)\Rightarrow A_{branca}=32-27 \therefore A_{branca}=5 \ u^2.
$$
Com isso, podemos concluir que a área em branco da figura [tex]C[/tex] é igual a [tex]5 \ u^2.[/tex]
Solução elaborada pelo COM Potências de Euler, com contribuições dos moderadores do Blog.
Solução 2
Para encontrar a área das regiões cinzas, podemos dividi-las em subfiguras cujas áreas sejam mais fáceis de se calcular. Teremos formas como triângulos [tex]\bigg(A_\Delta = \dfrac{b\cdot h}{2}\bigg)[/tex] e quadrados [tex](A_\square = l^2)[/tex], como mostrado nas figuras abaixo:
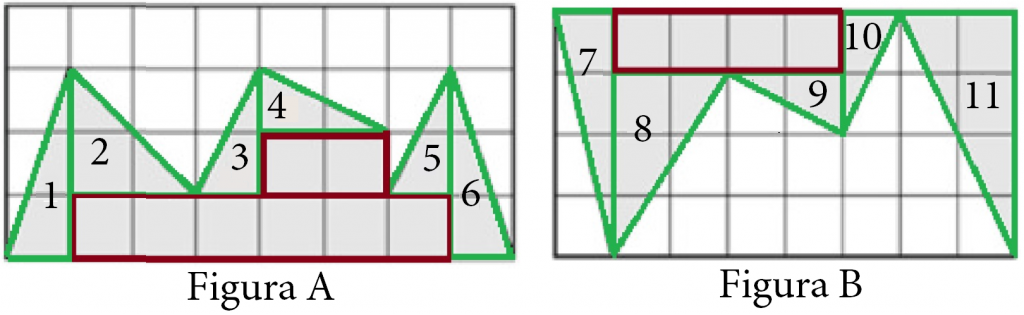
Usando a fórmula da área das figuras, chegamos aos seguintes resultados (lembrando que, como a área de todos os quadrados são iguais, basta multiplicar a área de um deles pela quantidade total de quadrados):
Área cinza da figura A
- Área dos Triângulos:
[tex]\qquad\begin {cases} \large 1 \implies \dfrac{1\cdot3}{2} = \dfrac{3}{2}\\
\large 2 \implies \dfrac{2\cdot2}{2} = 2\\
\large 3 \implies \dfrac{1\cdot2}{2} = 1\\
\large 4 \implies \dfrac{2\cdot1}{2} = 1\\
\large 5 \implies\dfrac{1\cdot2}{2} = 1\\
\large 6 \implies \dfrac{1\cdot3}{2} = \dfrac{3}{2} \end{cases}
[/tex]
- Área dos Quadrados:
[tex]\qquad\begin{cases}\large 1 \cdot 2 = 2 \\
\large 1 \cdot 6 = 6\end{cases}[/tex]
[tex]\qquad[/tex] Total: [tex]16[/tex].
Área cinza da figura B
- Área dos Triângulos:
[tex]\qquad\begin{cases} \large 7 \implies \dfrac{1\cdot 4}{2} = 2\\
\large 8 \implies \dfrac{2\cdot 3}{2} = 3\\
\large 9 \implies \dfrac{2\cdot 1}{2} =1\\
\large 10 \implies \dfrac{1\cdot 2}{2} = 1\\
\large 11 \implies \dfrac{2\cdot 4}{2} = 4 \end{cases}[/tex]
- Área dos Quadrados:
[tex]\qquad 1\cdot 4 = 4\\[/tex]
[tex]\qquad[/tex]Total: [tex]15[/tex].
Total da soma das áreas cinzas das duas figuras: [tex]16+15=31[/tex].
Dessa forma, a área preenchida em cinza na figura C seria [tex]31[/tex]. Por outro lado, a figura é formada pela junção de A e B, uma região de interseção surge e seu valor deve ser descontado do valor final da área cinza. Como o valor dessa interseção é [tex]4[/tex], basta descontarmos e obtemos [tex]27[/tex]. Como o total da área da figura C é [tex]32[/tex], isto é, [tex]4\cdot 8[/tex], basta subtrairmos o valor da área cinza encontrada do valor final, chegando a que a área branca na figura C é [tex]5[/tex].
Solução elaborada pelo COM Phidias, com contribuições dos moderadores do Blog.
Participaram da discussão os Clubes: Apótema Mineira ; Phidias ; Potências de Euler.



