Problema
(Indicado a partir do 9º ano do E. F.)
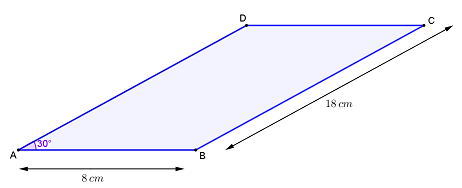
(GERONIMO, J.R; FRANCO, V.S, Geometria Plana e Espacial: um estudo axiomático, 2ed, EDUEM, Maringá, PR, 2010) Um paralelogramo tem dois lados medindo [tex]18~ cm[/tex] e [tex]8~ cm[/tex], e um ângulo medindo [tex]30^{\circ}[/tex].
Determine a área do paralelogramo.
 |
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex] Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex]. |
Solução
Considere o paralelogramo [tex]ABCD[/tex] com [tex]\overline {AD}[/tex] paralelo a [tex]\overline {BC}[/tex], [tex]D\widehat{A}B=30^\circ[/tex], [tex]AB= 8~cm[/tex] e [tex]BC=AD=18 ~cm\,.[/tex]
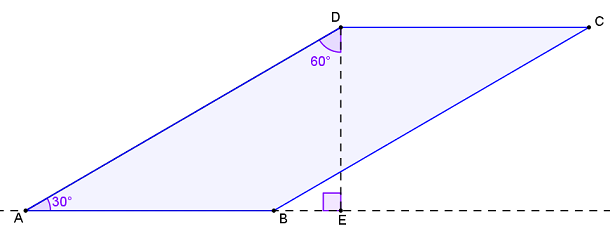
Traçando a altura por [tex]D[/tex] relativa ao lado [tex]\overline {AB}[/tex], obtemos o triângulo retângulo [tex]ADE[/tex].
Note que, como os ângulos [tex]D\widehat{A}E[/tex] e [tex]A\widehat{E}D[/tex] medem [tex]30^\circ[/tex] e [tex]90^\circ[/tex], respectivamente, concluímos que a medida do ângulo [tex] E\widehat{D}A[/tex] é [tex] 60^\circ[/tex]. (Lembre-se de que a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex].)
Agora, veja que
[tex]\qquad \dfrac{1}{2} = sen(30^\circ) = \dfrac{DE}{AD}= \dfrac{DE}{18} [/tex],
assim,
[tex]\qquad DE = \dfrac{18}{2}= 9~cm [/tex].
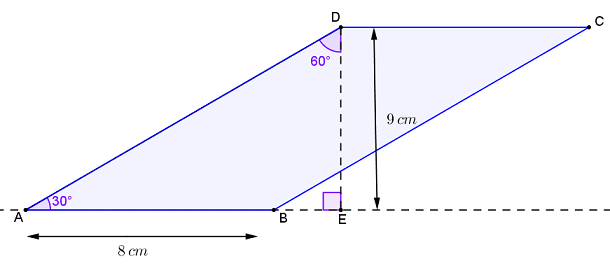
Logo, a área [tex]S[/tex] do paralelogramo [tex]ABCD[/tex] é dada por
[tex]\qquad S = AB \cdot DE = 8~cm \cdot 9~cm= \fcolorbox{black}{#eee0e5}{$72 \,cm^{2}$}\,. [/tex]
Solução elaborada pelos Moderadores do Blog.
