Nesta Sala vamos explorar prismas e cilindros e propormos uma estratégia para encontrar o volume de um cilindro.
Um prisma pode ter várias formas, dependendo dos polígonos que utilizamos como base.
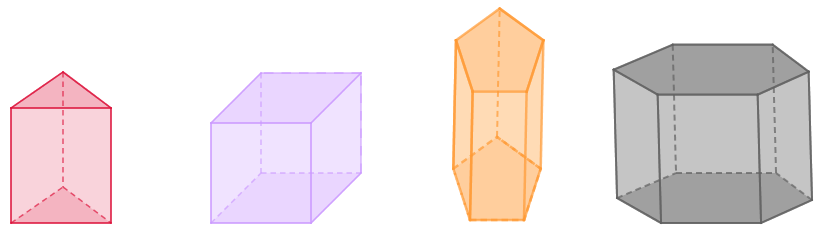
Além disso, mesmo escolhido o polígono da sua base, um prisma pode ser reto ou obliquo.
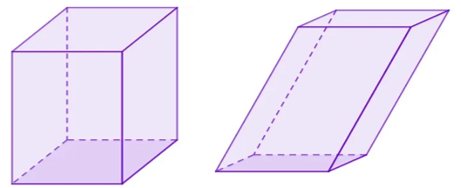
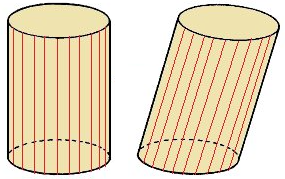
Por outro lado, os cilindros têm basicamente apenas duas formas: cilindro reto ou cilindro oblíquo, já que as bases dos cilindros são sempre círculos.
No entanto, observem que, embora não tenham arestas, o formato dos cilindros lembra o dos prismas, não é?
Podemos, então, explorar essa “semelhança de formatos” para determinar o volume de um cilindro.
Vamos lá!
Atividade 16 – Volume do cilindro
(a) (Aquecimento – áreas)
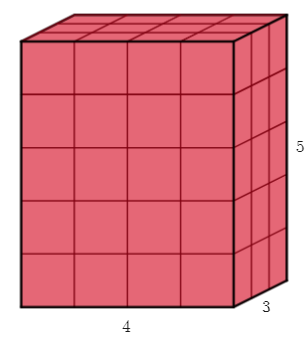
Quantos quadrados unitários serão necessários para preencher esse retângulo?
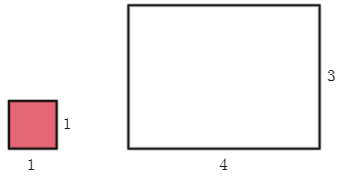
(b) (Aquecimento – volumes) Quantos cubos unitários serão necessários para preencher esse prisma retangular?
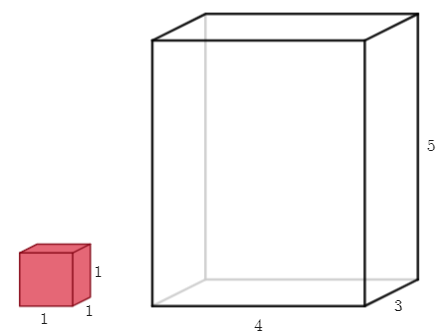
(c) Miriã calculou o volume desse prisma de três maneiras:
V = 12 ✕ 5 ; V = 15 ✕ 4 ; V = 20 ✕ 3.
Vamos nos concentrar na primeira igualdade utilizada pela Miriã.
Explique o que o 12 e o 5 representam na figura.
(d) Aqui está um novo prisma retangular.
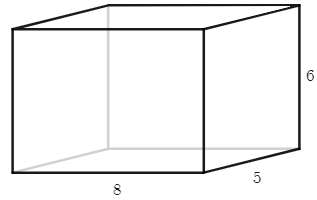
Use a estratégia de Miriã para escrever uma expressão para seu volume.
(e) Veja como Miriã descreveu sua estratégia para encontrar o volume de um prisma:
1. Encontre a área da base.
2. Multiplique essa área pela altura do objeto.
Para quais objetos abaixo vocês acreditam que a estratégia de Miriã funciona?
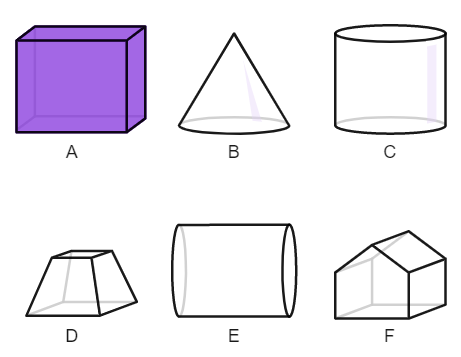
(f) A estratégia de Miriã funciona para cilindros!
Assim, o volume de um cilindro de altura h e raio da base r é dado por:
[tex]\qquad \boxed{V=\pi r^2\times h}\,.[/tex]
Calcule o volume deste cilindro:
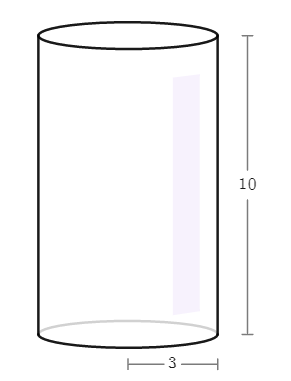
(g) Calcule os volumes destes cilindros:
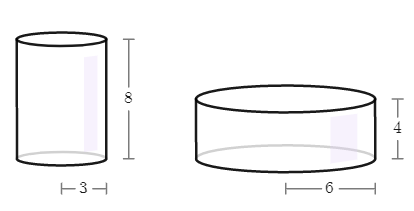
(h) No applet abaixo, mova os pontos verdes para criar dois cilindros de raios e alturas diferentes, porém com o mesmo volume.
(1) Esperem o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar um ponto verde, cliquem sobre ele com qualquer botão do mouse, mantenham o mouse pressionado e façam o movimento. (Se vocês estiverem utilizando um celular ou um tablet, basta tocar levemente no triângulo e fazer o movimento.)
(3) Se vocês estiverem usando um computador, vocês também poderão fazer os movimentos dos pontos verdes utilizando os seus teclados.
– Para movimentos horizontais, cliquem no ponto com o botão esquerdo do mouse. Em seguida, façam os movimentos utilizando as teclas “mover para a direita” ou “mover para a esquerda”.
– Para movimentos verticais, cliquem no ponto com o botão esquerdo do mouse. Em seguida, façam os movimentos utilizando as teclas “PgUp” ou “PgDn”.
(Para movimentos “mais finos”, mantenham a tecla Shift do teclado apertada enquanto vocês fazem o movimento.)
(4) Se quiserem voltar para a visualização inicial, cliquem nas setinhas circulares que aparecem no canto superior direito da janela do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Observações: O GeoGebra trabalha com arredondamentos. A visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
(i) Em um papel ou programa de computador, esbocem um prisma retangular e um cilindro. Escolham e rotulem as dimensões de cada sólido para que seus volumes sejam o mais próximo possível. Discutam.
Equipe COM – OBMEP