Problema
(Indicado a partir do 9º ano do E. F.)
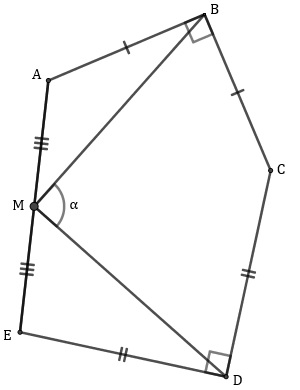
A partir da figura abaixo, calcule o ângulo [tex]\alpha[/tex], sabendo que [tex]ABCDE[/tex] é um pentágono, a medida dos ângulos [tex]\hat B\,[/tex] e [tex]\,\hat D[/tex] é [tex]90^\circ[/tex], [tex]AB=BC[/tex], [tex]CD= DE[/tex] e que [tex]M[/tex] é o ponto médio de [tex]\overline{AE}[/tex].

Lembretes
(1) Em todo pentágono a soma das medidas dos ângulos internos vale [tex]540^\circ.[/tex]
(2) Caso de congruência de triângulos L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes. (Se você não se lembra desse resultado, clique AQUI.)
(3) Em todo triângulo isósceles a mediana relativa à base é também uma altura.
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
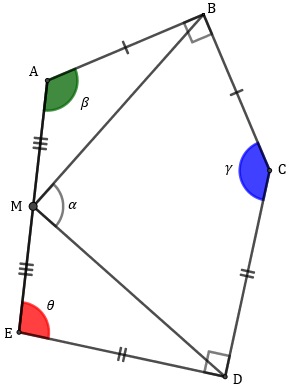
Como [tex]\hat B\,[/tex] e [tex]\,\hat D[/tex] são ângulos retos, pelo Lembrete (1), podemos afirmar que a soma das medidas dos ângulos [tex]\hat A[/tex], [tex]\hat C[/tex] e [tex]\hat E[/tex] vale [tex]360^\circ[/tex]. Denotaremos essas medidas de [tex]\beta[/tex], [tex]\gamma[/tex] e [tex]\theta[/tex], respectivamente.
Assim, [tex]\beta+\gamma+\theta=360^\circ\,. \qquad \textcolor{#800000}{(i)}[/tex]
Agora, vamos prolongar o segmento [tex]\overline{MB}[/tex] até um ponto [tex]P[/tex] de modo que [tex]\overline{MP}[/tex] seja congruente a [tex]\overline{MB}[/tex] e construir o triângulo [tex]MPE[/tex].
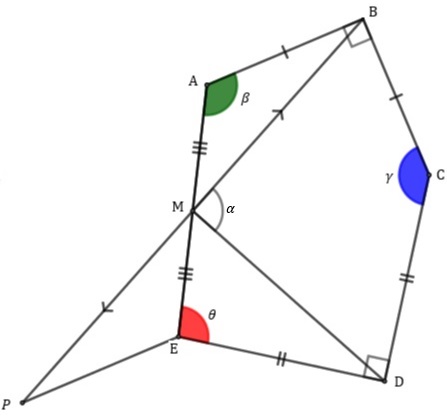
Note que os ângulos [tex]A\hat{M}B[/tex] e [tex]P\hat{M}E[/tex] são opostos pelo vértice, logo possuem a mesma medida.
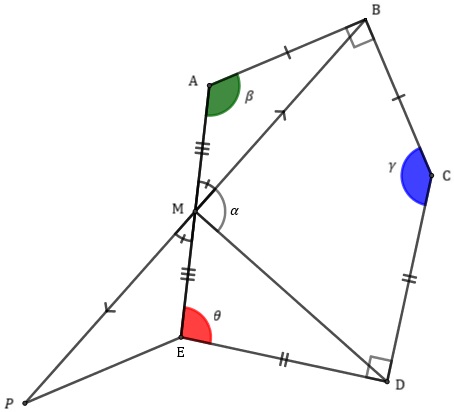
Dessa forma, pelo caso L.A.L ( Lembrete (2)), garantimos que os triângulos [tex]BMA[/tex] e [tex]PME[/tex] são congruentes; logo, o segmento [tex]\overline{AB}[/tex] é congruente ao segmento [tex]\overline{EP}[/tex] e os ângulos [tex]M\hat{A}B[/tex] e [tex]M\hat{E}P[/tex] possuem a mesma medida.
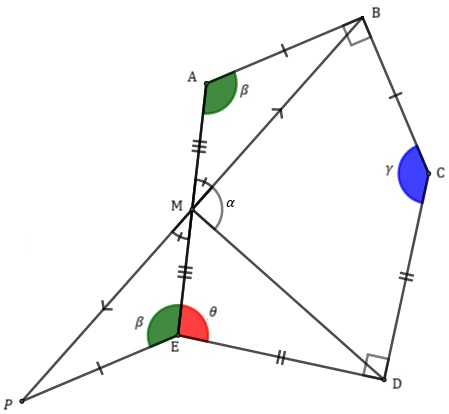
Note que, de acordo com a relação [tex]\textcolor{#800000}{(i)}[/tex], para termos um ângulo de uma volta completa em torno do ponto [tex]E[/tex], o ângulo [tex]P\hat{E}D[/tex] só pode ter medida [tex]\gamma[/tex].
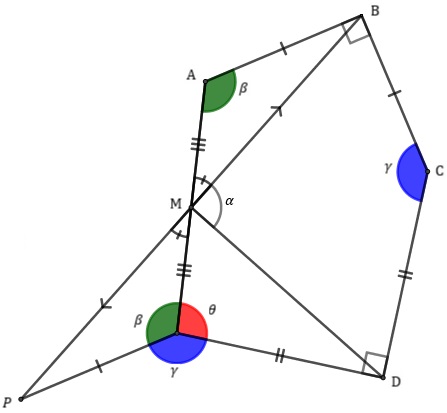
Traçando os segmentos [tex]\overline{PD}[/tex] e [tex]\overline{BD}[/tex], notamos, novamente pelo caso L.A.L., que os triângulos [tex]PED[/tex] e [tex]BCD[/tex] são congruentes.
Assim, os segmentos [tex]\overline{PD}[/tex] e [tex]\overline{BD}[/tex] são congruentes.
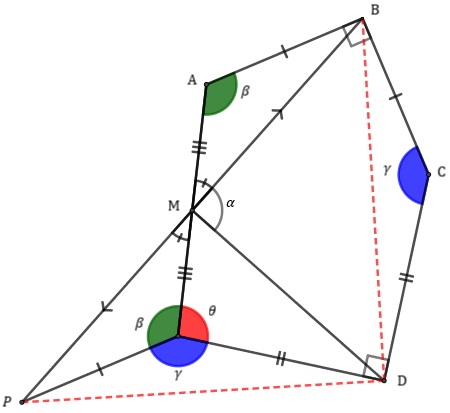
Com isso, o triângulo [tex]BDP[/tex] é isósceles (dois lados congruentes: [tex]BD=PD[/tex]) e [tex]\overline{DM}[/tex] é a mediana relativa à base.
Pelo Lembrete (3), [tex]\overline{DM}[/tex] também é altura; portanto, [tex]\,\fcolorbox{black}{#eee0e5}{$\alpha=90 ^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
