Problema
(A partir da 1ª série do E. M.)
As figuras a seguir são uma prova sem palavras de que [tex]\sqrt{2} [/tex] é irracional:
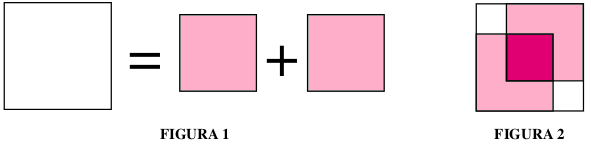
Vamos transformar essas figuras em uma prova com palavras!
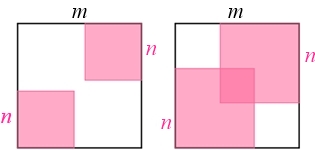
(a) Na Figura 1, vemos um quadrado branco e dois quadrados rosa claro iguais sendo relacionados geometricamente.
Considerando [tex]m[/tex] o comprimento do lado do quadrado maior e [tex]n[/tex] o comprimento dos lados dos quadrados menores, mostre que [tex]\dfrac{m}{n}=\sqrt{2}[/tex].
(b) Na Figura 2, vemos dois quadrados rosa claro iguais se sobrepondo no interior de um quadrado branco. Com isso, obtêm-se dois quadradinhos brancos e um quadrado rosa escuro, como ilustra a imagem.
Considerando que [tex]m[/tex] e [tex]n[/tex] são, respectivamente, os comprimentos dos lados do quadrado maior e dos dois quadrados rosa claro, encontre, em termos de [tex]m[/tex] e [tex]n[/tex], as medidas dos lados dos quadradinhos brancos e do quadrado rosa escuro.
(c) Utilizando a prova sem palavras acima, prove que [tex]\sqrt{2}[/tex] é irracional.
(Adaptado da OPM 2010)
Solução
(a) Sejam [tex]m[/tex] e [tex]n[/tex] as medidas dos lados do quadrado maior e dos quadrados menores, respectivamente, da Figura 1.
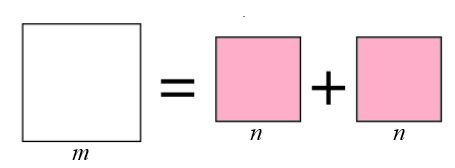
A igualdade ilustrada na Figura 1, nos permite concluir que [tex]m^2=n^2+n^2[/tex]; assim, [tex]m^2=2n^2\,.[/tex]
Extraindo a raiz quadrada de ambos os lados da igualdade [tex]m^2=2n^2[/tex], como temos medidas positivas, obtemos [tex]m=\sqrt{2}\,n[/tex], ou seja, [tex]\boxed{\dfrac{m}{n}=\sqrt{2}}\,.[/tex]
(b) Sejam [tex]m[/tex] e [tex]n[/tex], respectivamente, as medidas dos lados do quadrado maior e dos quadrados coloridos de rosa claro que aparecem na Figura 2.
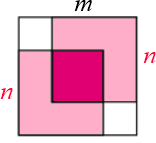
Como a medida do lado do quadrado externo é [tex]m[/tex] e a de cada quadrado rosa claro é [tex]n[/tex], então a medida do lado dos quadradinhos brancos é [tex]\boxed{m-n}\,.[/tex]
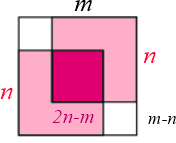
Agora, sendo [tex]x[/tex] a medida do lado do quadrado rosa escuro, utilizando a figura abaixo concluímos que [tex](m-n)+x+(m-n)=m[/tex]. Observe.
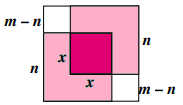
Assim, segue que:
[tex]\qquad m-n+x+m-n=m[/tex]
[tex]\qquad2m-2n+x=m[/tex]
[tex]\qquad x=m-2m+2n[/tex]
[tex]\qquad\boxed{\textcolor{red}{x=2n-m}}.[/tex]
(c) Estratégia: Vamos provar que [tex]\sqrt{2}[/tex] é irracional “por absurdo”, ou seja, vamos supor que [tex]\sqrt{2}[/tex] seja racional e chegar a uma contradição. Com isso podemos concluir que a suposição inicial que fizemos sobre a racionalidade de [tex]\sqrt{2}[/tex] está errada e, portanto, [tex]\sqrt{2}[/tex] é irracional.
Suponhamos, por absurdo, que [tex]\sqrt{2}[/tex] seja racional. Então existem inteiros positivos [tex]m[/tex] e [tex]n[/tex], primos entre si, tais que [tex]\dfrac{m}{n}=\sqrt{2}[/tex].
Sabemos que
[tex]\qquad \qquad 1 \lt \sqrt{2}\approx 1,4142 \lt 2[/tex];[tex] \qquad \qquad \textcolor{#800000}{(i)}[/tex]
assim, como [tex]\sqrt{2}\gt 1[/tex], segue que [tex]\dfrac{m}{n}\gt 1[/tex], ou seja, podemos concluir que [tex]m \gt n[/tex].
Dessa forma, é possível construir dois quadrados na cor rosa, ambos com lados medindo [tex]n[/tex], no interior de um quadrado branco com lados medindo [tex]m[/tex], de tal forma que:
- fixamos o vértice superior direito de um dos quadrados coloridos de rosa no vértice superior direito do quadrado branco;
- fixamos o vértice inferior esquerdo do segundo quadrado rosa no vértice inferior esquerdo do quadrado branco.
Mas precisamos fazer uma análise melhor dos valores [tex]m[/tex] e [tex]n[/tex], já que poderíamos, a princípio, ter duas situações: os quadrados na cor rosa se intersectam ou não.
Por [tex]\textcolor{#800000}{(i)}[/tex], sabemos que [tex] \sqrt{2} \lt 2[/tex]; então, [tex]\dfrac{m}{n} \lt 2[/tex] e, portanto, [tex]n \gt \dfrac{m}{2}.[/tex]
Podemos, então, afirmar que os quadrados coloridos de rosa construídos no interior do quadrado branco se intersectam.
Vocês podem visualizar geometricamente essa afirmação, utilizando o applet abaixo, antes de prosseguir com a leitura da solução.
Para entender melhor a afirmação de que os quadrados coloridos de rosa construídos no interior do quadrado branco se intersectam pois [tex]n \gt \dfrac{m}{2}[/tex], vocês podem utilizar o applet abaixo. É só movimentar o ponto vermelho para modificar o tamanho do quadrado menor e observar.
Instruções:
(1) Esperem o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar o ponto vermelho, cliquem sobre ele com qualquer botão do mouse, mantenham o mouse pressionado e façam o movimento. (Se vocês estiverem utilizando um celular ou um tablet, basta tocar levemente no triângulo e fazer o movimento.)
OBMEP_ srdg, criado com o GeoGebra
Pelo até aqui exposto, se [tex]\sqrt{2}=\dfrac{m}{n}[/tex], com [tex]m[/tex] e [tex]n[/tex] inteiros positivos primos entre si, conseguimos construir um quadrado com lados medindo [tex]m[/tex] e dois quadrados rosa claro, ambos com lados medindo [tex]n[/tex], posicionados como na Figura 2 do enunciado do problema.

Dessa forma, temos a seguinte relação entre as áreas dos quadrados que aparecem na figura:
Área do quadrado maior = Área dos quadrados rosa claro – Área do quadrado rosa escuro + Área dos quadradinhos brancos.
Vamos utilizar as relações estabelecidas no item (b) e reescrever essa igualdade a partir de [tex]m[/tex] e [tex]n[/tex]:
[tex]\qquad m^2=2n^2-(2n-m)^2+2(m-n)^2.\qquad \quad \textcolor{#800000}{(ii)}[/tex]
Por outro lado, como [tex]\sqrt{2}=\dfrac{m}{n}[/tex], então [tex]\textcolor{blue}{m^2=2n^2}[/tex]. Logo, de [tex]\textcolor{#800000}{(ii)}[/tex], segue que:
[tex]\qquad m^2=\textcolor{blue}{2n^2}-(2n-m)^2+2(m-n)^2\\
\qquad m^2=\textcolor{blue}{m^2}-(2n-m)^2+2(m-n)^2\\
\qquad 0=-(2n-m)^2+2(m-n)^2\\
\qquad(2n-m)^2=2(m-n)^2[/tex]
[tex] \qquad \dfrac{(2n-m)^2}{(m-n)^2}=2~[/tex] (Note que [tex]m\ne n[/tex].)
[tex]\qquad {\bigg(\dfrac{2n-m}{m-n}\bigg)^2}^{~}=2\\
\qquad \sqrt{\bigg(\dfrac{2n-m}{m-n}\bigg)^2}=\sqrt{2}\\
\qquad \bigg|\dfrac{2n-m}{m-n}\bigg|=\sqrt{2}\,.\quad \textcolor{#800000}{(iii)}[/tex]
Perceba, agora, que [tex]\dfrac{2n-m}{m-n}\gt0[/tex] (pois [tex]\textcolor{red}{x=2n-m}[/tex] é positivo e [tex]m\gt n[/tex]).
Então, segue de [tex]\textcolor{#800000}{(iii)}[/tex], que [tex]\boxed{\dfrac{2n-m}{m-n}=\sqrt{2}}.[/tex]
Mas, por hipótese, [tex]\boxed{\dfrac{m}{n}=\sqrt{2}}[/tex]; assim, [tex]\dfrac{2n-m}{m-n}=\dfrac{m}{n}[/tex], ou seja, as frações [tex]\dfrac{2n-m}{m-n}~[/tex] e [tex]~\dfrac{m}{n}[/tex] são equivalentes (representam o mesmo todo).
Para finalizar, vamos analisar a fração [tex]\dfrac{2n-m}{m-n}[/tex] e, para isso, vamos utilizar os dados do item (b), reunidos na última figura. Lembrem-se de que todos os números que nela aparecem são positivos, uma vez que são medidas de comprimentos.
|
[tex]\textcolor{#800000}{(iv)}[/tex] A fração [tex]\dfrac{2n-m}{m-n}[/tex] tem numerador e denominador ambos inteiros positivos.
[tex]\textcolor{#800000}{(v)}[/tex] Comparando os comprimentos [tex]2n-m~[/tex] e [tex]~m[/tex], concluímos que [tex]2n-m \lt m.[/tex] (Lembre-se de que [tex]n \gt \frac{m}{2}.[/tex])
[tex]\textcolor{#800000}{(vi)}[/tex] Comparando os comprimentos [tex]m-n~[/tex] e [tex]~n[/tex], concluímos que [tex]m-n \lt n.[/tex] |
 |
Mas as afirmações [tex]\textcolor{#800000}{(iv)}[/tex], [tex]\textcolor{#800000}{(v)}[/tex] e [tex]\textcolor{#800000}{(vi)}[/tex] mostram uma contradição, já que [tex]~\boxed{\dfrac{2n-m}{m-n}=\dfrac{m}{n}}~[/tex] e[tex]~[/tex] “[tex]m~[/tex] e [tex]n[/tex] são primos entre si”, ou seja, “a fração [tex]\dfrac{m}{n}[/tex] foi simplificada ao máximo”!
Conclui-se, então, que [tex]\sqrt{2}[/tex] é irracional.
Solução elaborada pelos Moderadores do Blog.
