Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
Determine o número natural de três algarismos que tem as seguintes propriedades:
- O algarismo das centenas é igual à soma dos outros dois algarismos.
- O quádruplo do algarismo das unidades é igual à soma dos outros dois algarismos.
Solução
Seja n=xyz o número natural que satisfaz as hipóteses do problema.
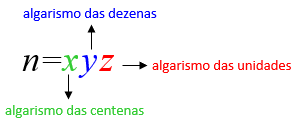
Assim:
x=y+z
4⋅z=y+x
e podemos, então, considerar o seguinte sistema:
{y+z=x(i)4⋅z=y+x.(ii)
Somando as equações (i) e (ii), obtemos
(y+z)+4⋅z=x+(y+x)
\qquad \cancel{y}+5\cdot z=2\cdot x+\cancel{y}
\qquad 5\cdot z=2\cdot x. \qquad \textcolor{#800000}{(iii)}
Como estamos lidando com números naturais, a igualdade \textcolor{#800000}{(iii)} \, nos mostra que o número 2\cdot x é um múltiplo de 5 e, como 2 é primo, na verdade x é múltiplo de 5.
Mas lembre-se de que x é um algarismo; assim, x=0 ou x=5. Mais ainda, x é o primeiro dígito de um número de três algarismos; com isso, x\ne 0 e, portanto, \boxed{x=5} \, .
Consequentemente, por \textcolor{#800000}{(iii)} \, , temos que 5z=10 e, então, \boxed{z=2} \, .
Finalmente, por \textcolor{#800000}{(i)} \, , segue que:
\qquad y=x-z
\qquad y=5-2
\qquad \boxed{y=3} \, .
Dessa forma, o número procurado é \, \fcolorbox{black}{#eee0e5}{$n=532$} \, .
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |