Problema
(Indicado a partir do 1º ano do E. M.)
Considere o gráfico de uma dada função [tex]f:[-5,5]\rightarrow \mathbb{R}[/tex] e responda se cada item abaixo é verdadeiro ou falso. Justifique.
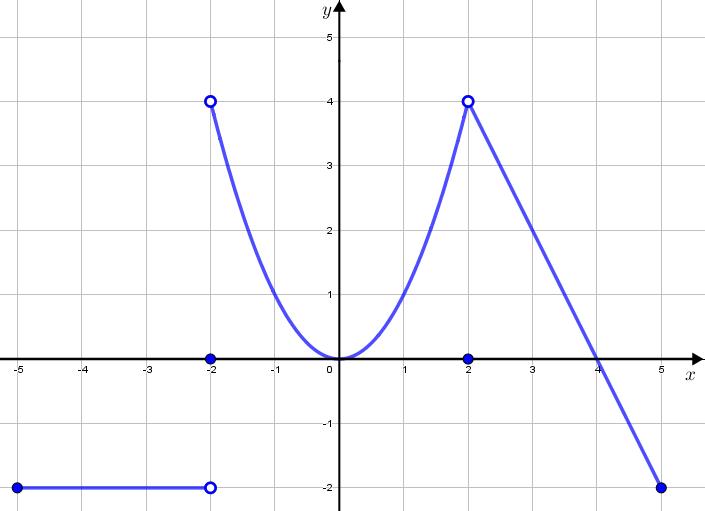
[tex]\textcolor{#800000}{(a)} \, f(-2)=f(2)[/tex]
[tex]\textcolor{#800000}{(b)}[/tex] A função [tex]f[/tex] possui exatamente uma raiz real.
[tex]\textcolor{#800000}{(c)}[/tex] A função [tex]g:[-5,5]\rightarrow \mathbb{R}[/tex] tal que [tex]g(x)=f(x)-2[/tex] possui exatamente duas raízes reais.
[tex]\textcolor{#800000}{(d)}[/tex] [tex](\underbrace{f\circ f \circ \cdots \circ f}_{n-1\, compostas})(-2)=-2[/tex] para qualquer valor natural de [tex]n[/tex].
Solução
[tex]\textcolor{#800000}{(a)}[/tex] Verdadeiro.
Como o gráfico contém os pontos [tex](-2,0)[/tex] e [tex](2,0)[/tex], temos [tex]f(-2)= 0[/tex] e [tex]f(2)= 0.[/tex]
Portanto, [tex]f(-2)=f(2)= 0. [/tex]
[tex]\textcolor{#800000}{(b)}[/tex] Falso.
Veja que o gráfico de [tex]f[/tex] corta o eixo das abscissas nos pontos [tex](-2,0),(0,0),(2,0),(4,0)[/tex] (pontos azuis sobre o eixo das abscissas, conforme indicado na figura a seguir).
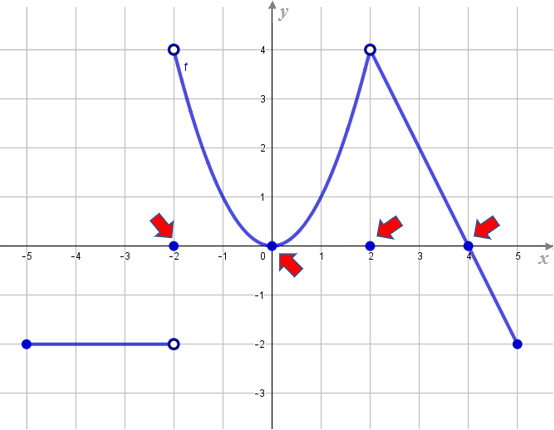
Assim, [tex]f(-2)=0 \, [/tex], [tex]f(0)=0 \, [/tex], [tex]f(2)=0 \, [/tex], [tex]f(4)=0 \, [/tex] e, portanto, a função [tex]f[/tex] possui quatro raízes: [tex]-2[/tex], [tex]2[/tex], [tex]0[/tex] e [tex]4[/tex].
[tex]\textcolor{#800000}{(c)}[/tex] Falso.
Sabemos que as raízes de [tex]g[/tex] são os valores de [tex]x[/tex] para os quais [tex]g(x)=0.[/tex] Assim, observe que:
[tex]\textcolor{#800000}{(i)} \, g(x)=0 \iff f(x)-2=0 \iff f(x)=2[/tex]
ou seja, [tex]g(x)=0[/tex] é equivalente a [tex]f(x)=2.[/tex]
[tex]\textcolor{#800000}{(ii)}[/tex] O gráfico da função [tex]f[/tex] nos indica que [tex]f(x)=2[/tex] para exatamente três valores de [tex]x.[/tex]
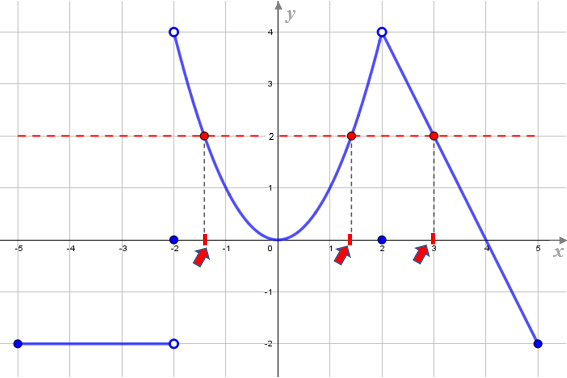
Assim, por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)} \, [/tex], concluímos que [tex]g[/tex] tem três raízes, pois as raízes de [tex]g[/tex] são os valores de [tex]x[/tex] para os quais [tex]f(x)=2.[/tex]
Se transladarmos o gráfico de [tex]f[/tex], podemos visualizar isso:
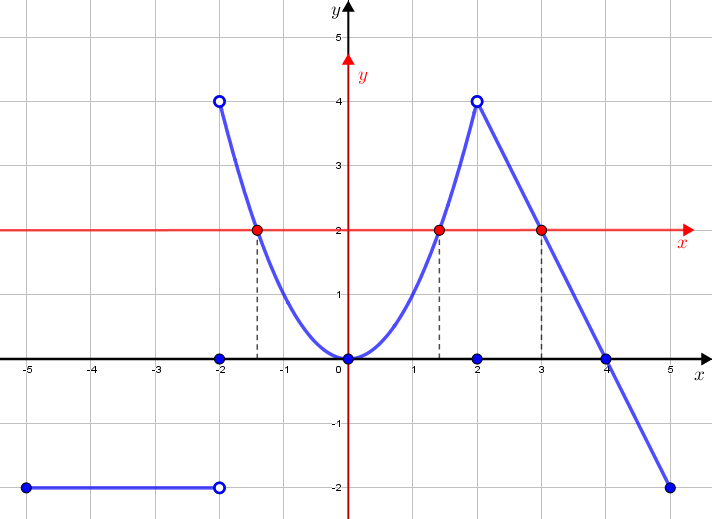
Nessa última figura, observe e compare as quatro raízes de [tex]f \, [/tex], no eixo [tex]x[/tex] inicial, e as três raízes de [tex]g \, [/tex], no eixo [tex]x[/tex] transladado .
[tex]\textcolor{#800000}{(d)}[/tex] Falso.
Temos [tex]\boxed{f(-2)=0}[/tex] e [tex]\boxed{f(0)=0}.[/tex] Assim:
- [tex]\textcolor{red}{\left(f\circ f \right)\left(-2\right)}=f\left(f\left(-2\right)\right)=f\left(0\right)=0[/tex]
- [tex]\textcolor{blue}{\left(f\circ f\circ f \right)\left(-2\right)}=f\left(\textcolor{red}{ \left(f\circ f \right)\left(-2\right)}\right)=f\left( \textcolor{red}{ 0}\right)=0[/tex]
- [tex]\textcolor{#32CD32}{\left(f\circ f\circ f\circ f \right)\left(-2\right)}=f\left( \textcolor{blue}{ \left(f\circ f\circ f \right)\left(-2\right)} \right)=f\left( \textcolor{blue}{ 0}\right)=0[/tex]
- [tex]\textcolor{#FF1493}{\left(f\circ f\circ f\circ f\circ f \right)\left(-2\right)}=f\left( \textcolor{#32CD32}{ \left(f\circ f\circ f\circ f \right)\left(-2\right)} \right)=f\left( \textcolor{#32CD32}{ 0}\right)=0[/tex]
- [tex]\left(f\circ f\circ f\circ f\circ f\circ f \right)\left(-2\right)=f\left( \textcolor{#FF1493}{ \left(f\circ f\circ f\circ f\circ f \right)\left(-2\right)} \right)=f\left( \textcolor{#FF1493}{0}\right)=0[/tex]
- [tex](\underbrace{f\circ f \circ \cdots \circ f}_{n-1\, compostas})(-2)=f(\textcolor{#00BFFF}{(\underbrace{f\circ f \circ \cdots \circ f}_{n-2\, compostas})(-2)})=f(\textcolor{#00BFFF}{0})=0.[/tex]
[tex]\qquad \qquad \quad \quad \vdots[/tex]
Assim, [tex]\boxed{(\underbrace{f\circ f \circ \cdots \circ f}_{n-1\, compostas})(-2)=0} \, [/tex], para qualquer valor natural [tex]n \, [/tex], [tex]n\geq 2[/tex].
Solução elaborada pelos Moderadores do Blog.
