Problema
(Indicado a partir do 1º ano do E. M.)
As funções [tex]f,g,h:\mathbb{R}\rightarrow\mathbb{R}[/tex] são definidas, respectivamente, por polinômios de grau 4, grau 1 e grau 2.
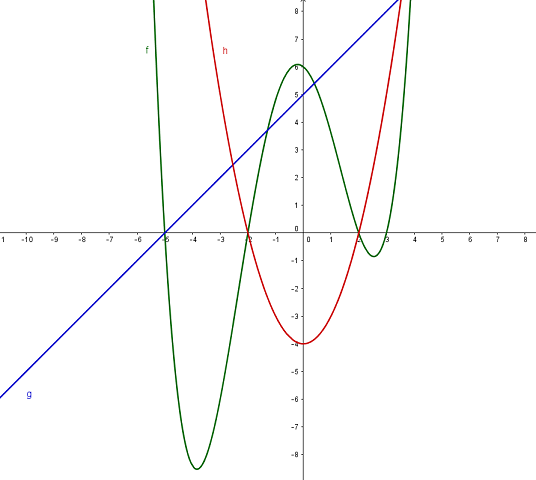
Os gráficos dessas funções estão representados geometricamente na figura que se segue, com as respectivas cores verde, azul e vermelho.
Se [tex]p[/tex] é a função definida como [tex]p(x)=\dfrac{f(x)g(x)}{h(x)},[/tex] determine os intervalos nos quais [tex]p(x)\le 0[/tex].
Solução
Como a função [tex]p[/tex] é definida a partir das funções [tex]f[/tex], [tex]g[/tex] e [tex]h[/tex], para determinarmos os valores de [tex]x[/tex] para os quais [tex]p(x)\le 0[/tex], devemos fazer um estudo dos sinais de cada uma dessas funções que definem [tex]p[/tex]. Para isso colhemos informações nos gráficos de [tex]f[/tex], [tex]g[/tex] e [tex]h[/tex] e construímos a tabela abaixo.
[tex]\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline & x \lt -5 & x=-5 & -5\lt x\lt -2 & x=-2 & -2\lt x\lt 2&x=2&2\lt x \lt 3&x=3&x \gt 3 \\
\hline \textcolor{darkgreen}{f(x)} & \textcolor{darkgreen}{+} & \textcolor{darkgreen}{0} & \textcolor{darkgreen}{-} & \textcolor{darkgreen}{0}&\textcolor{darkgreen}{+}&\textcolor{darkgreen}{0}&\textcolor{darkgreen}{-}&\textcolor{darkgreen}{0}&\textcolor{darkgreen}{+} \\
\hline \textcolor{blue}{g(x)} & \textcolor{blue}{-} & \textcolor{blue}{0} & \textcolor{blue}{+} & \textcolor{blue}{+}&\textcolor{blue}{+}&\textcolor{blue}{+}&\textcolor{blue}{+}&\textcolor{blue}{+}&\textcolor{blue}{+} \\
\hline \textcolor{red}{h(x)} & \textcolor{red}{+} & \textcolor{red}{+} & \textcolor{red}{+} & \textcolor{red}{0}&\textcolor{red}{-}&\textcolor{red}{0}&\textcolor{red}{+}&\textcolor{red}{+}&\textcolor{red}{+} \\
\hline \end{array}[/tex]
Antes de analisarmos o sinal da função [tex]p[/tex], observe que, como [tex]h(x)[/tex] está no denominador da regra que define [tex]p[/tex], a função [tex]p[/tex] não está definida para valores de [tex]x[/tex] tais que [tex]h(x)= 0[/tex]. Dessa forma, devemos ter [tex]h(x)\neq 0[/tex], o que significa [tex]x\neq\pm 2[/tex] e, portanto, o domínio da função [tex]p[/tex] é [tex]\boxed{D_p=\{x\in\mathbb{R} \, | \, x\neq\pm2\}}[/tex].
Feita essa observação, a partir da tabela acima, podemos concluir que o sinal da função [tex]p[/tex] varia de acordo com a próxima tabela.
[tex]\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline & x \lt -5 & x=-5 & -5 \lt x \lt -2 & x=-2 & -2 \lt x \lt 2&x=2&2 \lt x \lt3&x=3&x \gt 3 \\
\hline p(x)& – & 0 & – &\not\exists &-&\not\exists &-&0&+ \\
\hline
\end{array}[/tex]
Como queremos os intervalos em que [tex]p(x)\le 0[/tex], temos como solução:
[tex]\qquad \qquad S=\{x\in\mathbb{R} \, | \, x \le 3 [/tex] e [tex] x\neq\pm2\}[/tex].
Podemos, ainda, expressar o conjunto [tex]S[/tex] utilizando a notação de intervalos:
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$S=] \, -\infty \, , \, -2 \, [ \, \cup \, ] \, -2 \, , \, 2 \, [ \, \cup \, ] \, 2 \, , \, 3 \, ]$}[/tex].

Solução elaborada pelos Moderadores do Blog.
