Problema
(Indicado a partir do 8º ano do E. F.)
Seja [tex]A[/tex] a soma dos algarismos de [tex](\underbrace{99\dots9}_{2016})^2[/tex].
Determine a soma dos algarismos de [tex]A[/tex].
Solução 1
Seja [tex]N=(\underbrace{99\dots9}_{2016})^2[/tex]. É claro que a ideia não é calcularmos a potência [tex](\underbrace{99\dots9}_{2016})^2[/tex]. (Ufa!!!)
Observe inicialmente que
[tex]\qquad \begin{align*}
N=(\underbrace{999\dots9}_{2016\ \text{ noves}})^2 & =(10^{2016}-1)^2\\
&=\left(10^{2016}\right)^2-2\cdot 10^{2016} \cdot 1+\left(1 \right)^2\\
&=10^{4032}-2\cdot 10^{2016}+1 \\
&=\boxed{10^{2016} \cdot\left(10^{2016}-2\right)+1} \quad \quad \color{#800000}{(i)}\end{align*}[/tex]
Para simplificar as contas, vamos fazer [tex]x=10^{2016}-2[/tex], reescrever [tex]\boxed{10^{2016}\cdot\left(10^{2016}-2\right)+1}[/tex] como [tex]\boxed{10^{2016}\cdot x+1}[/tex] e analisar a expressão [tex]10^{2016}\cdot x+1[/tex].
- Ao multiplicarmos um número por [tex]10^{2016}[/tex], acrescentamos [tex]2016[/tex] zeros à direita desse número; assim:
[tex]\qquad 10^{2016}\cdot x=x\underbrace{000\dots 0}_{2016\ \text{ zeros}}. \quad \quad[/tex] [tex](ii)[/tex] - Agora, vamos efetuar a soma [tex] x\underbrace{000\dots 0}_{2016\ \text{ zeros}}+1[/tex]:
[tex]\begin{array}{ccccccc}
&x&0&0&\dots &0&0\\
+&&&&&&1\\
\hline
&x&0&0&\dots&0&1\\
\end{array}[/tex]
assim, [tex] x\underbrace{000\dots 0}_{2016\ \text{ zeros}}+1=x\underbrace{000\dots 0}_{2015\ \text{ zeros}}1.\quad \quad[/tex] [tex](iii)[/tex]
Logo, por [tex](ii)[/tex] e [tex](iii)[/tex],
[tex]\qquad \boxed{10^{2016}\cdot x+1}=x\underbrace{000\dots 0}_{2015\ \text{ zeros}}1,[/tex]
ou seja,
[tex]\qquad \boxed{10^{2016} \cdot \left(10^{2016}-2\right)+1}=\boxed{10^{2016}\cdot x+1}=x\underbrace{000\dots 0}_{2015\ \text{ zeros}}1[/tex]. [tex]\quad \quad(iv)[/tex]
Como, por [tex](i)[/tex] e [tex](iv)[/tex], temos que
[tex]\qquad N=x\underbrace{000\dots 0}_{2015\ \text{ zeros}}1, \quad \quad[/tex] [tex](v)[/tex]
resta-nos apenas calcular o número [tex]x=10^{2016}-2[/tex] para obtermos [tex]N[/tex].
- Sabemos que [tex] 10^{2016}=1\underbrace{000\dots 0}_{2016\ \text{ zeros}};[/tex] vamos, então, efetuar a diferença [tex]x=10^{2016}-2[/tex]:
[tex]\begin{array}{ccccccc}
&1&0&0&\dots &0&0\\
-&&&&&&2\\
\hline
& &9&9&\dots&9&8\\
\end{array}[/tex]
Com isso
[tex]\qquad x=10^{2016}-2= \underbrace{999…9}_{2015\ \text{ noves}}8,\quad \quad[/tex] [tex](vi)[/tex]
e, dessa forma, por [tex](v)[/tex] e [tex](vi)[/tex],
[tex]\qquad N=(\underbrace{99\dots9}_{2016})^2=\underbrace{999…9}_{2015\ \text{ noves}}8 \underbrace{000\dots 0}_{2015\ \text{ zeros}}1.[/tex]
Portanto, a soma dos algarismos de [tex]N[/tex] é
[tex]\qquad A=2015\times 9+8+1=18144[/tex].
Sendo [tex]A=18144[/tex], a soma dos algarismos de [tex]A[/tex] é [tex]1+8+1+4+4=18.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Primeiramente, devemos observar que [tex](\underbrace{99\dots9}_{2016})^2[/tex] é igual a [tex](10^{2016} – 1)^2[/tex].
Deste modo, podemos aplicar produtos notáveis:
- [tex](10^{2016} – 1)^2 = 10^{4032} – 2(10^{2016}) + 1^2[/tex]
Por agora, vamos esquecer o “[tex]1^2[/tex]” e focar na subtração:
- A diferença [tex]10^{4032} – 2(10^{2016})[/tex] é a diferença entre “o [tex]1[/tex] seguido de [tex]4032[/tex] zeros” e “o [tex]2[/tex] seguido de [tex]2016[/tex] zeros”, o que resulta em um número que começa com [tex]2015[/tex] noves seguidos de um [tex]8[/tex] e [tex]2016[/tex] zeros.
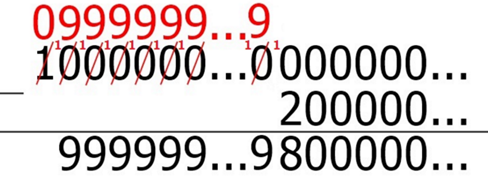
Logo,
[tex]\qquad (\underbrace{99\dots9}_{2016})^2=10^{4032} – 2(10^{2016})+1^2=\underbrace{999…9}_{2015\ \text{ noves}}8\underbrace{000…0}_{2015\ \text{ zeros}}1[/tex],
donde a soma de seus algarismos, [tex]A[/tex], é igual a [tex]2016\cdot0 + 8 + 2015\cdot9 + 1[/tex].
O [tex]8[/tex] pode ser somado com o [tex]1[/tex], formando mais um [tex]9[/tex]; logo, temos [tex]A=2016\cdot9[/tex], que resulta em [tex]A=18144[/tex].
Se [tex]A[/tex] é igual a [tex]18144[/tex], a soma dos algarismos de [tex]A[/tex] é igual a [tex]18[/tex].
Solução elaborada pelo Clube 1uik, com contribuições dos Moderadores do Blog.
